题目内容
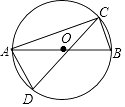
【题目】已知,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P. 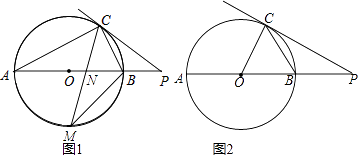
(1)如图①,若∠COB=2∠PCB,求证:直线PC是⊙O的切线;
(2)如图②,若点M是AB的中点,CM交AB于点N,MNMC=36,求BM的值.
【答案】
(1)证明:∵OA=OC,
∴∠A=∠ACO.
∴∠COB=2∠ACO.
又∵∠COB=2∠PCB,
∴∠ACO=∠PCB.
∵AB是⊙O的直径,
∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°,即OC⊥CP.
∵OC是⊙O的半径,
∴PC是⊙O的切线
(2)解:连接MA、MB.(如图)
∵点M是弧AB的中点,
∴ ![]() ,
,
∴∠ACM=∠BAM.
∵∠AMC=∠AMN,
∴△AMC∽△NMA.
∴ ![]() .
.
∴AM2=MCMN.
∵MCMN=36,
∴AM=6,
∴BM=AM=6.

【解析】(1)利用半径OA=OC可得∠COB=2∠A,然后利用∠COB=2∠PCB即可证得结论,再根据圆周角定理,易得∠PCB+∠OCB=90°,即OC⊥CP;故PC是⊙O的切线;(2)连接MA,MB,由圆周角定理可得∠ACM=∠BAM,进而可得△AMC∽△NMA,故AM2=MCMN;等量代换可得MNMC=BM2=AM2 , 代入数据即可得到结论.
【考点精析】通过灵活运用圆周角定理和切线的判定定理,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线即可以解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目