题目内容
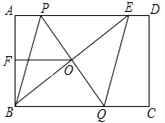
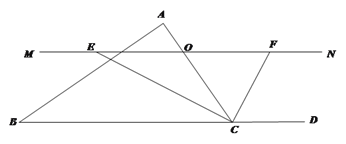
【题目】已知△ABC中,点O是边AC上的一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF.
(2)试确定点O在边AC上的位置,使四边形AECF是矩形,并加以证明.
(3)在(2)的条件下,且△ABC满足 ____________时,矩形AECF是正方形.
【答案】∠BAC=90°
【解析】分析:(1)由平行线的性质和角平分线的性质,推出∠ECB=∠CEO,∠GCF=∠CFO,∠ECB=∠ECO,∠GCF=∠OCF,通过等量代换即可推出∠CEO=∠ECO,∠CFO=∠OCF,便可确定OC=OE,OC=OF,可得OE=OF;
(2)当O点运动到AC的中点时,四边形AECF为矩形,根据矩形的判定定理(对角线相等且互相平分的四边形为矩形),结合(1)所推出的结论,即可推出OA=OC=OE=OF,求出AC=EF后,即可确定四边形AECF为矩形;
(3)当△ABC是直角三角形时,四边形AECF是正方形,根据(2)所推出的结论,由AC⊥BC,MN∥BC,确定AC⊥EF,即可推出结论.
详解:(1)∵CE是∠ACB的平分线,∴∠ACE=∠BCE.
∵MN∥BC,∴∠FEC=∠BCE,∴∠ACE=∠FEC,∴OE=OC,
同理可证OF=OC,
∴OE=OF;
(2)当点O运动到AC中点时,四边形AECF是矩形.
∵OA=OC,OE=OF,∴四边形AECF平行四边形.
∵OE=OC,∴OA=OC=OE=OF,∴AC=EF,
∴平行四边形AECF是矩形;
(3)当点O运动到AC的中点,且△ABC满足∠ACB=90°时,四边形AECF是正方形.理由如下:
∵当点O运动到AC的中点时,AO=CO.
又∵EO=FO,∴四边形AECF是平行四边形.
∵FO=CO,∴AO=CO=EO=FO,∴AO+CO=EO+FO,即AC=EF,∴四边形AECF是矩形.
∵MN∥BC,当∠ACB=90°,则∠AOF=∠COE=∠COF=∠AOE=90°,∴AC⊥EF,∴四边形AECF是正方形;
故答案为:∠ACB=90°.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的液体,并用流量、速度、密度三个概念描述车流的基本特征。其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度;密度(辆/千米)指通过道路指定断面单位长度内的车辆数,为配合大数据治堵行动,测得某路段流量q与速度v之间的部分数据如下表:
速度v(千米/小时) | … | 5 | 10 | 20 | 32 | 40 | 48 | … |
流量q(辆/小时) | … | 550 | 1000 | 1600 | 1792 | 1600 | 1152 | … |
(1)根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是(只需填上正确答案的序号)① ![]() ②
② ![]() ③
③ ![]()
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速为多少时,流量达到最大?最大流量是多少?
(3)已知q,v,k满足 ![]() ,请结合(1)中选取的函数关系式继续解决下列问题:
,请结合(1)中选取的函数关系式继续解决下列问题:
①市交通运行监控平台显示,当 ![]() 时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值