题目内容
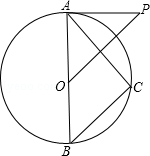
【题目】如图,在等边△ABC中,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点,判断下列说法错误的是( ) 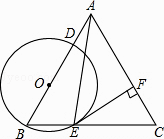
A.若EF⊥AC,则EF是⊙O的切线
B.若EF是⊙O的切线,则EF⊥AC
C.若BE=EC,则AC是⊙O的切线
D.若BE= ![]() EC,则AC是⊙O的切线
EC,则AC是⊙O的切线
【答案】C
【解析】解:A、如图1,连接OE, 
则OB=OE,
∵∠B=60°
∴∠BOE=60°,
∵∠BAC=60°,
∴∠BOE=∠BAC,
∴OE//AC,
∵EF⊥AC,
∴OE⊥EF,
∴EF是⊙O的切线
∴A选项正确;
B、∵EF是⊙O的切线,
∴OE⊥EF,
由A知:OE//AC,
∴AC⊥EF,
∴B选项正确;
C、∵∠B=60°,OB=OE,
∴BE=OB,
∵BE=CE,
∴BC=AB=2BO,
∴AO=OB,
如图2,过O作OH⊥AC于H,
∵∠BAC=60°,
∴OH= ![]() AO≠OB,
AO≠OB,
∴C选项错误;
D、如图2,∵BE= ![]() EC,
EC,
∴CE= ![]() BE,
BE,
∵AB=BC,BO=BE,
∴AO=CE= ![]() OB,
OB,
∴OH= ![]() AO=OB,
AO=OB,
∴AC是⊙O的切线,
∴D选项正确.
故选C.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目