题目内容
【题目】如图,在矩形ABCD中,AB=8,AD=12,过点A、D两点的⊙O与BC边相切于点E,则⊙O的半径为 . 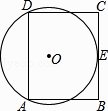
【答案】![]()
【解析】解:连结EO并延长交AD于F,如图, 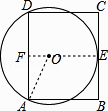
∵⊙O与BC边相切于点E,
∴OE⊥BC,
∵四边形ABCD为矩形,
∴BC//AD,
∴OF⊥AD,
∴AF=DF= ![]() AD=6,
AD=6,
易得四边形ABEF为矩形,则EF=AB=8,设⊙O的半径为r,则OA=r,OF=8﹣r,
在Rt△AOF中,∵OF2+AF2=OA2 ,
∴(8﹣r)2+62=r2 , 解得r= ![]() ,
,
即⊙O的半径为 ![]() .
.
所以答案是 ![]() .
.
【考点精析】关于本题考查的矩形的性质和切线的性质定理,需要了解矩形的四个角都是直角,矩形的对角线相等;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目