��Ŀ����
����Ŀ��ij��˾�����һ���Ʒ��ÿ���ɱ���50Ԫ���������ڼ䣬���г����飬���۵�����60Ԫʱ��ÿ���������250���������۵���ÿ����1Ԫ��ÿ������۳�5������˾�������۵���x��Ԫ��������60Ԫ�����г�Ҫ��x���ó���100Ԫ��
��1�����ÿ���������y�����������۵���x��Ԫ��֮��ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2�����ÿ�����������W��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ���������xΪ����ʱ��ÿ��������������������ֵ��
��3�����ù�˾Ҫ��ÿ�������������4000Ԫ����ÿ����ܳɱ�������6250Ԫ�������۵���x��Ϳɶ�Ϊ����Ԫ��
���𰸡���1��y����5x+550����60��x��100������2����x��80ʱ��y�����ֵΪ4500Ԫ����3������x��Ϳɶ�Ϊ85Ԫ��
��������
��1���ɡ�ÿ����1Ԫ����������5������֪������ΪxԪʱ����5��x��60�����������ӵļ�������ԭ�������ɱ�ʾ��������y��
��2�����ݡ�ÿ������=���ۼ۩��ɱ��������������г���������ʽ���ٶԶ��κ��������䷽���������������ֵ��
��3����W=4000�����x��ֵ���ٸ���������ͼ��д��W��4000ʱx��ȡֵ��Χ���ٸ����ܳɱ�������6250�г�����ʽ��������������ʽ�������x��ȡֵ��Χ���Ӷ�ȷ��x����Сֵ��
��1��y=250��5��x��60������y=��5x+550��60��x��100����
��2��W=��x��50������5x+550������y=��5x2+800x��27500��
�䷽�ã�W=��5��x��80��2+4500��
��a=��5���������߿������£��൱x=80ʱ��y�����ֵΪ4500Ԫ��
��3����W=4000ʱ����5��x��80��2+4500=4000����ã�x1=70��x2=90��
��������ͼ���֪����W��4000Ԫʱ��x��ȡֵ��ΧΪ70��x��90��
�֡�50����5x+550����6250����ã�x��85����xȡֵ��ΧΪ85��x��90�����x��Ϳɶ�Ϊ85Ԫ��
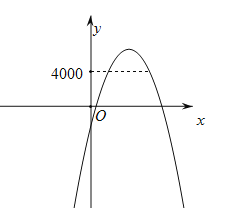

 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�