Question

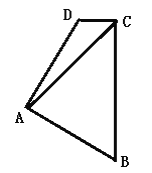
【题目】发现：已知△ABC中，AE是△ABC的角平分线，∠B＝72°，∠C＝36°

（1）如图1，若AD⊥BC于点D，求∠DAE的度数；

（2）如图2，若P为AE上一个动点（P不与A、E重合），且PF⊥BC于点F时，∠EPF＝　 　°．

（3）探究：如图2△ABC中，已知∠B，∠C均为一般锐角，∠B＞∠C，AE是△ABC的角平分线，若P为线段AE上一个动点（P不与E重合），且PF⊥BC于点F时，请写出∠EPF与∠B，∠C的关系，并说明理由．

Answer 1

【答案】（1）18°（2）18°（3）∠EPF＝

【解析】

（1）利用三角形内角和定理和角平分线定义求出∠BAE＝36°，然后根据直角三角形的性质求出∠BAD＝18°，问题得解；

（2）首先求出∠AEB＝72°，然后根据直角三角形的性质求解即可；

（3）如图2，同（1）（2）步骤可得结论．

（1）∠BAC＝180°－36°－72°＝72°，

∵AE是△ABC的角平分线，

∴∠BAE＝36°，

∵AD⊥BC，

∴∠BAD＝90°－72°＝18°，

∴∠DAE＝∠BAE -∠BAD =36°－18°＝18°；

（2）∵∠B＝72°，∠BAE＝36°，

∴∠AEB＝180°-72°-36°=72°，

∵PF⊥BC，

∴在三角形EPF中，∠EPF＝90°－∠AEB＝90°－72°＝18°；

（3）∠EPF＝，

理由：∵AE为角平分线，

∴∠BAE＝（180°－∠B－∠C），

∴∠AEB＝180°－∠B－∠BAE＝180°－∠B－（180°－∠B－∠C）＝90°－∠B ＋∠C，

在三角形EPF中，∠EPF＝90°－∠AEB＝90°－（90°－∠B ＋∠C）＝.