��Ŀ����
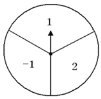
����Ŀ����ͼ��һת�̱��ȷֳ��������Σ�����ֱ����-1��1��2�е�һ������ָ��̶���ת��ת�̺���������ֹͣ����ʱij�����λ�ǡ��ͣ��ָ����ָ��λ�ã�����Ӧ�õ���������ϵ����� ��ָ��ǡ��ָ�ڵȷ����ϣ�����ָ���ұߵ����Σ�����ת��һ��ת�̣������õ�����Ϊk����ʹ����������![]() ��ͼ���ڵ�һ�������ĸ����Ƕ��٣���С����С�������Ϸ��ÿ�˸�ת������ת�̣��������������Ļ�Ϊ��������С��Ӯ���������������Ļ�Ϊ��������С��Ӯ�����Ǹ���ƽ����Ϸ����˵�����ɣ�����������״ͼ���б��ķ�����
��ͼ���ڵ�һ�������ĸ����Ƕ��٣���С����С�������Ϸ��ÿ�˸�ת������ת�̣��������������Ļ�Ϊ��������С��Ӯ���������������Ļ�Ϊ��������С��Ӯ�����Ǹ���ƽ����Ϸ����˵�����ɣ�����������״ͼ���б��ķ�����
���𰸡�![]() ������ƽ�����ɼ�����
������ƽ�����ɼ�����
��������
���ݷ��������������ʿ�֪����k��0��ͼ���ڵ�һ�������ޣ��ɴ˽�ɣ�
�������������б�������״ͼ���������еȿ��ܵij��ֽ����Ȼ����ݸ��ʹ�ʽ����������¼��ĸ��ʣ�
��2��1��0��-1��
�෴��������![]() ��ͼ���ڵ�һ�������ĸ�����
��ͼ���ڵ�һ�������ĸ�����![]() ��
��
�б��ã�
�� �� | -1 | 1 | 2 |
-1 | ��-1��-1�� | ��-1��1�� | ��-1��2�� |
1 | ��1��-1�� | ��1��1�� | ��1��2�� |
2 | ��2��-1�� | ��2��1�� | ��2��2�� |
�ɱ���֪������9�ֿ��ܵĽ����ÿ�ֽ�����ֵĿ�������ͬ�����������������Ļ�Ϊ�����Ľ����5�֣������������Ļ�Ϊ�����Ľ����4�֣�
��P��С��Ӯ��=![]() ��P��С��Ӯ��=
��P��С��Ӯ��=![]() ��
��
��С��Ӯ�ĸ��ʲ�����С��Ӯ�ĸ��ʣ�
�������Ϸ����ƽ��

 ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д� ���ɿ��ñ���ϵ�д�
���ɿ��ñ���ϵ�д�