题目内容
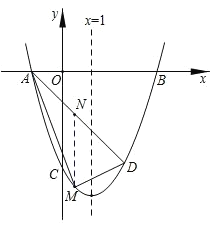
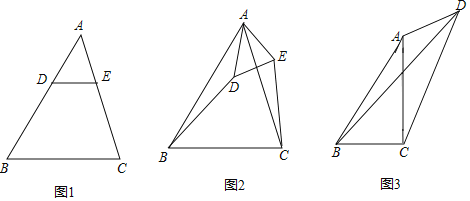
【题目】如图,抛物线y=x2+bx+c与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,﹣3),对称轴为x=1,点D与C关于抛物线的对称轴对称.
(1)求抛物线的解析式及点D的坐标;
(2)点P是抛物线上的一点,当△ABP的面积是8时,求出点P的坐标;
(3)点M为直线AD下方抛物线上一动点,设点M的横坐标为m,当m为何值时,△ADM的面积最大?并求出这个最大值.

【答案】(1)y=x2﹣2x﹣3,D(2,﹣3);(2)P(1﹣2![]() ,4)或(1+2
,4)或(1+2![]() ,4)或(1,﹣4);(3)m=
,4)或(1,﹣4);(3)m=![]() 时,△AMD的最大值为
时,△AMD的最大值为![]()
【解析】
(1)由抛物线y=x2+bx+c的对称轴为x=1,求出b的值,再由点C的坐标求出c的值即可;
(2)先求出点A,点B的坐标,设点P的坐标为(s,t),因为△ABP的面积是8,根据三角形的面积公式可求出t的值,再将t的值代入抛物线解析式即可;
(3)求出直线AD的解析式,过点M作MN∥y轴,交AD于点N,则点M的坐标为(m,m2﹣2m﹣3),点N的坐标为(m,﹣m﹣1),用含m的代数式表示出△AMN的面积,配方后由二次函数的性质即可得出结论.
(1)∵抛物线y=x2+bx+c的对称轴为x=1,
∴![]() 1,
1,
∴b﹣=2.
∵抛物线与y轴交于点C(0,﹣3),
∴c=﹣3,
∴抛物线的解析式为y=x2﹣2x﹣3,
∴抛物线的对称轴为直线x=1.
∵点D与C关于抛物线的对称轴对称,
∴点D的坐标为(2,﹣3);
(2)当y=0时,x2﹣2x﹣3=0,
解得:x1=﹣1,x2=3,
∴点A的坐标为(﹣1,0),点B的坐标为(3,0),
∴AB=3﹣(﹣1)=4,
设点P的坐标为(s,t).
∵△ABP的面积是8,
∴![]() AB|yP|=8,
AB|yP|=8,
即![]() 4|t|=8,
4|t|=8,
∴t=±4,
①当t=4时,s2﹣2s﹣3=4,
解得:,s1=![]() ,s2=
,s2=![]() ,
,
∴点P的坐标为(![]() ,4)或(
,4)或(![]() ,4);
,4);
②当t=﹣4时,s2﹣2s﹣3=﹣4,
解得:,s1=s
∴点P的坐标为(1,﹣4);
综上所述:当△ABP的面积是8时,点P的坐标为(![]() ,4)或(
,4)或(![]() ,4)或(1,﹣4);
,4)或(1,﹣4);
(3)设直线AD的解析式为y=kx+b1,
将A(﹣1,0),D(2,﹣3)代入y=kx+b1,
得: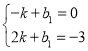 ,
,
解得: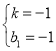 ,
,
∴直线AD的解析式为y=﹣x﹣1,
过点M作MN∥y轴,交AD于点N.
∵点M的横坐标是m(﹣1<m<2),
∴点M的坐标为(m,m2﹣2m﹣3),点N的坐标为(m,﹣m﹣1),
∴MN=﹣m﹣1﹣(m2﹣2m﹣3)=﹣m2+m+2,
∴S△AMD=S△AMN+S△DMN
![]() MN(m+1)
MN(m+1)![]() MN(2﹣m)
MN(2﹣m)
![]() MN
MN
![]() (﹣m2+m+2)
(﹣m2+m+2)
![]() (m
(m![]() )2
)2![]() ,
,
∵![]() 0,﹣1
0,﹣1![]() 2,
2,
∴当m![]() 时,S△AMD
时,S△AMD![]() ,
,
∴当m![]() 时,△AMD的最大值为
时,△AMD的最大值为![]() .
.