题目内容
【题目】在平面直角坐标系中,已知,A(2![]() ,0),C(0,﹣1),若P为线段OA上一动点,则CP+
,0),C(0,﹣1),若P为线段OA上一动点,则CP+![]() AP的最小值为_____.
AP的最小值为_____.
【答案】![]()
【解析】
可以取一点D(0,1),连接AD,作CN⊥AD于点N,PM⊥AD于点M,根据勾股定理可得AD=3,证明△APM∽△ADO得![]() ,PM=
,PM=![]() AP.当CP⊥AD时,CP+
AP.当CP⊥AD时,CP+![]() AP=CP+PM的值最小,最小值为CN的长.
AP=CP+PM的值最小,最小值为CN的长.
如图,
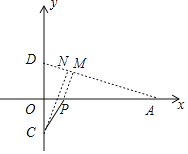
取一点D(0,1),连接AD,作CN⊥AD于点N,PM⊥AD于点M,
在Rt△AOD中,
∵OA=2![]() ,OD=1,
,OD=1,
∴AD=![]() =3,
=3,
∵∠PAM=∠DAO,∠AMP=∠AOD=90°,
∴△APM∽△ADO,
∴![]() ,
,
即![]() ,
,
∴PM=![]() AP,
AP,
∴PC+![]() AP=PC+PM,
AP=PC+PM,
∴当CP⊥AD时,CP+![]() AP=CP+PM的值最小,最小值为CN的长.
AP=CP+PM的值最小,最小值为CN的长.
∵△CND∽△AOD,
∴![]() ,
,
即![]()
∴CN=![]() .
.
所以CP+![]() AP的最小值为
AP的最小值为![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】某林业部门要考察某幼苗的成活率,于是进行了试验,下表中记录了这种幼苗在一定条件下移植的成活情况,则下列说法不正确的是( )
移植总数 | 400 | 1500 | 3500 | 7000 | 9000 | 14000 |
成活数 | 369 | 1335 | 3203 | 6335 | 8073 | 12628 |
成活的频率 | 0923 | 0.890 | 0915 | 0.905 | 0.897 | 0.902 |
A.由此估计这种幼苗在此条件下成活的概率约为0.9
B.如果在此条件下再移植这种幼苗20000株,则必定成活18000株
C.可以用试验次数累计最多时的频率作为概率的估计值
D.在大量重复试验中,随着试验次数的增加,幼苗成活的频率会越来越稳定,因此可以用频率估计概率