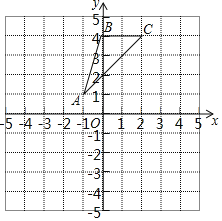题目内容
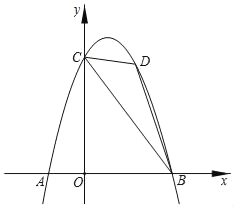
【题目】如图,在平面直角坐标系中,![]() ,则经过
,则经过![]() 三点的圆弧所在圆的圆心
三点的圆弧所在圆的圆心![]() 的坐标为__________;点
的坐标为__________;点![]() 坐标为
坐标为![]() ,连接
,连接![]() ,直线
,直线![]() 与
与![]() 的位置关系是___________.
的位置关系是___________.

【答案】(2,0) 相切
【解析】
由网格容易得出AB的垂直平分线和BC的垂直平分线,它们的交点即为点M,根据图形即可得出点M的坐标;由于C在⊙M上,如果CD与⊙M相切,那么C点必为切点;因此可连接MC,证MC是否与CD垂直即可.可根据C、M、D三点坐标,分别表示出△CMD三边的长,然后用勾股定理来判断∠MCD是否为直角.
解:如图,作线段AB,CD的垂直平分线交点即为M,由图可知经过A、B、C三点的圆弧所在圆的圆心M的坐标为(2,0).
连接MC,MD,
∵MC2=42+22=20,CD2=42+22=20,MD2=62+22=40,
∴MD2=MC2+CD2,∴∠MCD=90°,
又∵MC为半径,
∴直线CD是⊙M的切线.

故答案为:(2,0);相切.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某林业部门要考察某幼苗的成活率,于是进行了试验,下表中记录了这种幼苗在一定条件下移植的成活情况,则下列说法不正确的是( )
移植总数 | 400 | 1500 | 3500 | 7000 | 9000 | 14000 |
成活数 | 369 | 1335 | 3203 | 6335 | 8073 | 12628 |
成活的频率 | 0923 | 0.890 | 0915 | 0.905 | 0.897 | 0.902 |
A.由此估计这种幼苗在此条件下成活的概率约为0.9
B.如果在此条件下再移植这种幼苗20000株,则必定成活18000株
C.可以用试验次数累计最多时的频率作为概率的估计值
D.在大量重复试验中,随着试验次数的增加,幼苗成活的频率会越来越稳定,因此可以用频率估计概率