题目内容
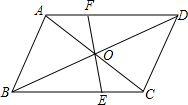
如图,E、F是?ABCD对角线AC上的两点,且BE∥DF.
求证:(1)△ABE≌△CDF;
(2)∠1=∠2.

求证:(1)△ABE≌△CDF;
(2)∠1=∠2.

证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
∵BE∥DF,
∴∠BEF=∠DFE.
∴∠AEB=∠CFD,
∴△ABE≌△CDF(AAS).
(2)由△ABE≌△CDF得,BE=DF
∵BE∥DF,
∴四边形BEDF是平行四边形
∴∠1=∠2.
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,

∵BE∥DF,
∴∠BEF=∠DFE.
∴∠AEB=∠CFD,
∴△ABE≌△CDF(AAS).
(2)由△ABE≌△CDF得,BE=DF
∵BE∥DF,
∴四边形BEDF是平行四边形
∴∠1=∠2.

练习册系列答案
相关题目