题目内容
【题目】如图,线段AB是⊙O的直径,弦CD⊥AB,∠CAB=40°,则∠ABD与∠AOD分别等于( ) 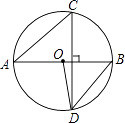
A.40°,80°
B.50°,100°
C.50°,80°
D.40°,100°
【答案】B
【解析】解:∵CD⊥AB,
∴∠AEC=90°,
∵∠CAB=40°,
∴∠C=50°,
∴∠ABD=∠C=50°,
∵OB=OD,
∴∠ABD=∠ODB=50°,
∴∠AOD=∠ABD+∠ODB=100°,
故选B.
求出∠AEC=90°,根据三角形内角和定理求出∠C=50°,根据圆周角定理即可求出∠ABD,根据OB=OD得出∠ABD=∠ODB=50°,根据三角形外角性质求出即可.本题考查了圆周角定理,垂径定理的应用,能熟记圆周角定理的内容是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目