题目内容
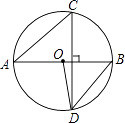
【题目】如图,一次函数y=ax+b的图象与反比例函数y= ![]() (x>0)的图象交于点P(m,4),与x轴交于点A(﹣3,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于点P(m,4),与x轴交于点A(﹣3,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC. 
(1)求反比例函数与一次函数的解析式;
(2)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
【答案】
(1)解:∵AC=BC,CO⊥AB,A(﹣3,0),
∴O为AB的中点,即OA=OB=3,
∴P(3,4),B(3,0),
将P(3,4)代入反比例解析式得:k=12,即反比例解析式为y= ![]() .
.
将A(﹣3,0)与P(3,4)代入y=ax+b得: ![]() ,
,
解得: ![]() ,
,
∴一次函数解析式为y= ![]() x+2
x+2
(2)解:如图所示,
把y=2代入y= ![]() 中,得x=6,得D(6,2),
中,得x=6,得D(6,2),
PB垂直且平分CD,
则四边形BCPD为菱形.
则点D(6,2)
【解析】(1)先根据题意得出P点坐标,把点P(3,4)代入反比例函数y= ![]() 即可得出k的值,再将A、P两点的坐标代入y=ax+b求出kb的值,故可得出一次函数的解析式,进而得出结论;(2)先求得y=2时,x=6,再根据菱形的判定即可求解.本题考查的是反比例函数综合题,涉及到一次函数与反比例函数图象上点的坐标特点、菱形的判定与性质等知识,难度适中.
即可得出k的值,再将A、P两点的坐标代入y=ax+b求出kb的值,故可得出一次函数的解析式,进而得出结论;(2)先求得y=2时,x=6,再根据菱形的判定即可求解.本题考查的是反比例函数综合题,涉及到一次函数与反比例函数图象上点的坐标特点、菱形的判定与性质等知识,难度适中.
【考点精析】通过灵活运用菱形的判定方法,掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形即可以解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目