题目内容
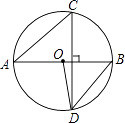
【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(﹣1,0),B(0,﹣ ![]() ),C(2,0),其对称轴与x轴交于点D
),C(2,0),其对称轴与x轴交于点D
(1)求二次函数的表达式及其顶点坐标;
(2)若P为y轴上的一个动点,连接PD,则 ![]() PB+PD的最小值为;
PB+PD的最小值为;
(3)M(x,t)为抛物线对称轴上一动点
①若平面内存在点N,使得以A,B,M,N为顶点的四边形为菱形,则这样的点N共有 个;
②连接MA,MB,若∠AMB不小于60°,求t的取值范围.
【答案】
(1)
解:由题意 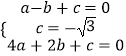 解得
解得 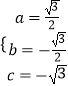 ,
,
∴抛物线解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() ,
,
∵y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() =
= ![]() (x﹣
(x﹣ ![]() )2﹣
)2﹣ ![]() ,
,
∴顶点坐标( ![]() ,﹣
,﹣ ![]() )
)
(2)![]()
(3)
① 5
②解:如图,RT△AOB中,∵tan∠ABO= ![]() =
= ![]() ,
,
∴∠ABO=30°,
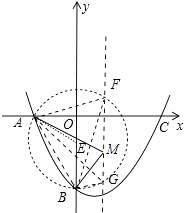
作AB的中垂线与y轴交于点E,连接EA,则∠AEB=120°,
以E为圆心,EB为半径作圆,与抛物线对称轴交于点F、G.
则∠AFB=∠AGB=60°,从而线段FG上的点满足题意,
∵EB= ![]() =
= ![]() ,
,
∴OE=OB﹣EB= ![]() ,
,
∵F( ![]() ,t),EF2=EB2,
,t),EF2=EB2,
∴( ![]() )2+(t+
)2+(t+ ![]() )2=(
)2=( ![]() )2,
)2,
解得t= ![]() 或
或 ![]() ,
,
故F( ![]() ,
, ![]() ),G(
),G( ![]() ,
, ![]() ),
),
∴t的取值范围 ![]() ≤t≤
≤t≤ ![]()
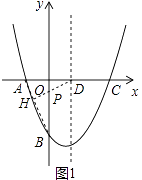
【解析】【解析】解:(2)如图1中,连接AB,作DH⊥AB于H,交OB于P,
此时 ![]() PB+PD最小.
PB+PD最小.
理由:∵OA=1,OB= ![]() ,
,
∴tan∠ABO= ![]() =
= ![]() ,
,
∴∠ABO=30°,
∴PH= ![]() PB,
PB,
∴ ![]() PB+OD=PH+PD=DH,
PB+OD=PH+PD=DH,
∴此时 ![]() PB+PD最短(垂线段最短).
PB+PD最短(垂线段最短).
在RT△ADH中,∵∠AHD=90°,AD= ![]() ,∠HAD=60°,
,∠HAD=60°,
∴sin60°= ![]() ,
,
∴DH= ![]() ,
,
∴ ![]() PB+PD的最小值为
PB+PD的最小值为 ![]() .
.
所以答案是 ![]() .
.
(3)①以A为圆心AB为半径画弧与对称轴有两个交点,
以B为圆心AB为半径画弧与对称轴也有两个交点,
线段AB的垂直平分线与对称轴有一个交点,
所以满足条件的点M有5个,即满足条件的点N也有5个,
所以答案是5.
(1)利用待定系数法转化为解方程组解决问题.(2)如图1中,连接AB,作DH⊥AB于H,交OB于P,此时 ![]() PB+PD最小.最小值就是线段DH,求出DH即可.(3)①先在对称轴上寻找满足△ABM是等腰三角形的点M,由此即可解决问题.②作AB的中垂线与y轴交于点E,连接EA,则∠AEB=120°,以E为圆心,EB为半径作圆,与抛物线对称轴交于点F、G.则∠AFB=∠AGB=60°,从而线段FG上的点满足题意,求出F、G的坐标即可解决问题.本题考查二次函数综合题、锐角三角函数、最短问题、圆等知识,解题的关键是掌握待定系数法确定函数解析式,学会利用垂线段最短解决实际问题中的最短问题,学会添加辅助线,构造圆解决角度问题,属于中考压轴题.
PB+PD最小.最小值就是线段DH,求出DH即可.(3)①先在对称轴上寻找满足△ABM是等腰三角形的点M,由此即可解决问题.②作AB的中垂线与y轴交于点E,连接EA,则∠AEB=120°,以E为圆心,EB为半径作圆,与抛物线对称轴交于点F、G.则∠AFB=∠AGB=60°,从而线段FG上的点满足题意,求出F、G的坐标即可解决问题.本题考查二次函数综合题、锐角三角函数、最短问题、圆等知识,解题的关键是掌握待定系数法确定函数解析式,学会利用垂线段最短解决实际问题中的最短问题,学会添加辅助线,构造圆解决角度问题,属于中考压轴题.
【考点精析】根据题目的已知条件,利用垂线段最短和锐角三角函数的增减性的相关知识可以得到问题的答案,需要掌握连接直线外一点与直线上各点的所有线段中,垂线段最短;现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用;当角度在0°~90°之间变化时:(1)正弦值随着角度的增大(或减小)而增大(或减小)(2)余弦值随着角度的增大(或减小)而减小(或增大)(3)正切值随着角度的增大(或减小)而增大(或减小)(4)余切值随着角度的增大(或减小)而减小(或增大).

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案