题目内容
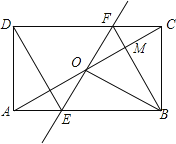
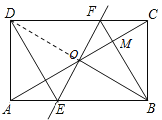
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连结BF,交AC于点M,连结DE,BO.若∠BOC=60°,FO=FC,则下列结论:①AE=CF;②BF垂直平分线段OC;③△EOB≌△CMB;④四边形是BFDE菱形.其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
【答案】C
【解析】
利用ASA定理证明△AOE≌△COF,从而判断①;利用线段垂直平分线的性质的逆定理可得结论②;在△EOB和△CMB中,对应直角边不相等,则两三角形不全等,从而判断③;连接BD,先证得BO=DO, OE=OF,进而证得OB⊥EF,因为BD、EF互相垂直平分,即可证得四边形EBFD是菱形,从而判断④.
解:∵矩形ABCD中,O为AC中点
∴∠DCA=∠BAC,OA=OC,∠AOE=∠COF
∴△AOE≌△COF
∴AE=CF,故①正确
∵矩形ABCD中,O为AC中点,
∴OB=OC,
∵∠COB=60°,
∴△OBC是等边三角形,
∴OB=BC,
∵FO=FC,
∴FB垂直平分OC,故②正确;
∵△BOC为等边三角形,FO=FC,
∴BO⊥EF,BF⊥OC,
∴∠CMB=∠EOB=90°,
∴BO≠BM,
∴△EOB与△CMB不全等;故③错误;
连接BD,
∵四边形ABCD是矩形,
∴AC=BD,AC、BD互相平分,
∵O为AC中点,
∴BD也过O点,且BO=DO
由①可知△AOE≌△COF,∴OE=OF
∴四边形EBFD是平行四边形
由②可知,OB=CB,OF=FC
又∵BF=BF
∴△OBF≌△OCF
∴BD⊥EF
∴平行四边形EBFD是菱形,故④正确
所以其中正确结论的个数为3个;
故选:C.

练习册系列答案
相关题目