题目内容
如图,⊙O的弦AB∥CD,直径BE平分AD于点G,交弦CD于点H,过点B作BF∥AD交CD延长线于点F.
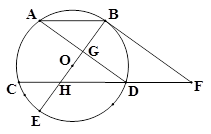
小题1:(1)求证:BF与⊙O相切;
小题2:(2)求证:DF=DH;
小题3:(3)若弦AB=5㎝,AD=8㎝,求⊙O的半径.

小题1:(1)求证:BF与⊙O相切;
小题2:(2)求证:DF=DH;
小题3:(3)若弦AB=5㎝,AD=8㎝,求⊙O的半径.
小题1:(1)证明:∵直径BE平分弦AD于点G,
∴BE⊥AD,AG="DG " ①. ...……….1’
∵BF∥AD,
∴∠1=∠2=90°.
∴直径BE⊥BF.
∴BF与⊙O相切.
小题2:(2)证明:∵AB∥CD,BF∥AD,
∴四边形ABFD是平行四边形,...…………………………………….3’
∠A=∠4②.
∴DF=AB.
由①、②及∠3=∠2,得△ABG≌△DHG. ……………………….4’
∴AG=DH.
∴DH="DF. "
小题3:(3)解:连结OA.
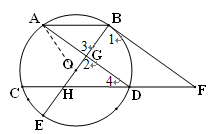
∵AD=8cm,∴AG=4cm.
∵AB=5cm,∠3=90°,
∴BG="4cm. " ...………………………………………….6’
设OA=OB=xcm,则OG=(x-3)cm
∵OA2=OG2+AG2,∴x2=42+(x-3)2. ...………………………………….7’
解得x=
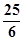 ...………………………………………….8’
...………………………………………….8’∴半径为
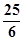 .
.略

练习册系列答案
相关题目
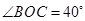 ,则∠C的度数等于( )
,则∠C的度数等于( )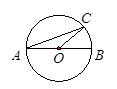
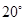
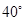
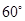
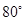
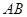 是⊙O的直径,
是⊙O的直径,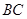 切⊙O于点
切⊙O于点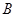 ,且
,且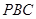 为等腰三角形,若存在,有几个符合条件的点
为等腰三角形,若存在,有几个符合条件的点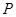 ,并分别求出点
,并分别求出点