题目内容
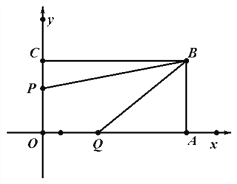
【题目】如图所示,A(2,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(a,b),且a=![]() +
+![]() -6
-6
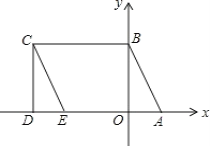
(1)求点C的坐标;
(2)求点E的坐标;
(3)点P是CE上一动点,设∠CBP=x°,∠PAD=y°,∠BPA=z°,确定x,y,z之间的数量c关系,并证明你的结论
【答案】(1)(﹣6,4);(2)(﹣4,0);(3)x+y=z;见解析.
【解析】
(1)直接利用二次根式的性质得出a,b的值,即可得出答案;
(2)利用平移的性质得出点E的坐标;
(3)利用平行线的性质分析得出答案.
解:(1)∵![]()
∴b=4,a=﹣6,
∵点C的坐标为(a,b),
∴点C的坐标为:(﹣6,4);
(2)∵点B在y轴上,点C的坐标为:(﹣6,4),
∴B点向左平移了6个单位长度,
∴A(2,0),向左平移6个单位得到:(﹣4,0)
∴点E的坐标为:(﹣4,0);
故答案为:(﹣4,0);
(3)x+y=z.证明如下:
如图,过点P作PN∥CD,
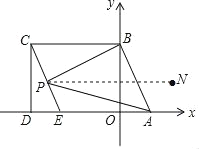
∴∠CBP=∠BPN
又∵BC∥AE,
∴PN∥AE
∴∠EAP=∠APN
∴∠CBP+∠EAP=∠BPN+∠APN=∠APB,
即x+y=z.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目