题目内容
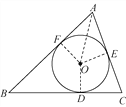
【题目】如图,△ABC外切于⊙O,切点分别为点D,E,F,∠A=60°,BC=7,⊙O的半径为![]() .求:(1)求BF+CE的值; (2)求△ABC的周长.
.求:(1)求BF+CE的值; (2)求△ABC的周长.

【答案】(1)7(2)20
【解析】
(1)、根据切线长定理得到BF=BD,CE=CD,代入求出即可;(2)、根据切线长定理得到AE=AF,求出∠OAE=30°,根据含30度得直角三角形和勾股定理求出OA、AE,即可求出答案.
(1)如答图,连结OF,OE,OD, ∵△ABC外切于⊙O,切点分别为D,E,F,
∴BF=BD,CE=CD, ∴BF+CE=BD+CD=BC=7;
(2)如答图,连结OA. ∵△ABC外切于⊙O,切点分别为D,E,F,
∴∠OEA=90°,∵AF=AE,AO=AO,FO=EO, ∴△AFO≌△AEO,∴∠OAE=![]() ∠BAC=30°,
∠BAC=30°,
∴OA=2OE=2![]() ,由勾股定理,得AE=AF=
,由勾股定理,得AE=AF=![]() =
=![]() =3,
=3,
∴△ABC的周长是AB+BC+AC=AF+AE+CE+BF+BC=3+3+7+7=20.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目