题目内容
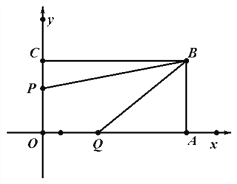
【题目】如图长方形OABC的位置如图所示,点B的坐标为(8,4),点P从点C出发向点O移动,速度为每秒1个单位;点Q同时从点O出发向点A移动,速度为每秒2个单位,设运动时间为t(0≤t≤4)
(1)填空:点A的坐标为 ,点C的坐标为 ,点P的坐标为 (用含t的代数式表示)
(2)当t为何值时,P、Q两点与原点距离相等?
(3)在点P、Q移动过程中,四边形OPBQ的面积是否变化?说明理由。
【答案】(1)A(8,0);B(0,4);C(0,4-t);(2)![]() ;(3)(3)四边形OPBQ的面积不变.理由见解析.
;(3)(3)四边形OPBQ的面积不变.理由见解析.
【解析】试题分析:(1)根据长方形的对边相等,分别写出点A、C的坐标即可,用t表示出PC的长,即可得OP的长,从而求得点P的坐标;(2)用t表示出OQ的长,根据OP=OQ列出方程,解方程求得t值即可;(3)设运动时间为t,表示出CP、AQ,再根据S四边形OPBQ=S矩形ABCD-S△ABQ-S△BPC列式整理即可得解.
试题解析:
(1)填空:点A的坐标为 (8,0) ,点C的坐标为 (0,4) ,
点P的坐标为 (0,4-t) .(用含t的代数式表示)

依题意可知:OP=4-t,OQ=2t,若OP=OQ,则有:4-t=2t
解之得,t=![]() .
.
∴当t=![]() 时,点P和点Q到原点的距离相等
时,点P和点Q到原点的距离相等
四边形OPBQ的面积不变.理由如下:

∴四边形OPBQ的面积不变

练习册系列答案
相关题目