Question

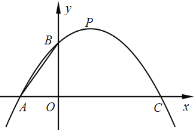
【题目】如图，抛物线y=ax2+c经过点A（0，2）和点B（-1，0）．

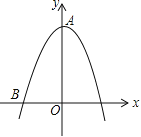
（1）求此抛物线的解析式；

（2）将此抛物线平移，使其顶点坐标为（2，1），平移后的抛物线与x轴的两个交点分别为点C，D（点C在点D的左边），求点C，D的坐标；

（3）将此抛物线平移，设其顶点的纵坐标为m，平移后的抛物线与x轴两个交点之间的距离为n，若1＜m＜3，直接写出n的取值范围．

Answer 1

【答案】（1）y=-2x2+2；（2）C（ 2-，0），D（2+，0）（3）＜n＜．

【解析】

试题（1）把点A、B的坐标分别代入函数解析式，列出关于a、c的方程组，通过解方程求得它们的值；

（2）根据平移的规律写出平移后抛物线的解析式，然后令y=0，则解关于x的方程，即可求得点C、D的横坐标；

（3）根据根与系数的关系来求n的取值范围；

试题解析：（1）∵抛物线y=ax2+c经过点A（0，2）和点B（-1，0）．

∴

解得：

∴ 此抛物线的解析式为y=-2x2+2；

（2）∵ 此抛物线平移后顶点坐标为（2，1），

∴ 抛物线的解析式为y=-2（x-2）2+1

令y=0，即-2（x-2）2+1=0

解得 x1=2+，x2=2-．

∵ 点C在点D的左边

∴ C（ 2-，0），D（2+，0）

（3）＜n＜．