��Ŀ����
����Ŀ����ͼ��ʾ�����κ���![]() ��ͼ����
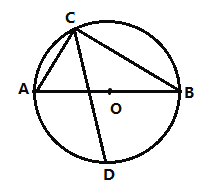
��ͼ����![]() �ύ��A��B���㣬��y�ύ�ڵ�C�����е�B��x����������ϣ���C��y����������ϣ��߶�OB��OC�ij���OB<OC)�Ƿ���
�ύ��A��B���㣬��y�ύ�ڵ�C�����е�B��x����������ϣ���C��y����������ϣ��߶�OB��OC�ij���OB<OC)�Ƿ���![]() ������������A������Ϊ(-6,0)��
������������A������Ϊ(-6,0)��
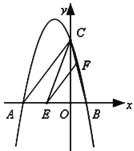
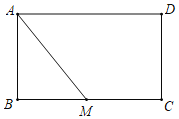
��1����˶��κ����ı���ʽ��
��2������E���߶�AB�ϵ�һ�����㣨���A��B���غϣ�������E��EF��AC��BC�ڵ�F������CE.��AE�ij�Ϊm����CEF�����Ϊs����S��![]() ֮��ĺ�����ϵʽ����д���Ա���
֮��ĺ�����ϵʽ����д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3���ڣ�2���Ļ�������˵��S�Ƿ�������ֵ�������ڣ������S�����ֵ���������ʱ��E�����꣬�жϴ�ʱ��BCE����״���������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��S��
����2��S��![]() ��m��ȡֵ��Χ��0��m��8����3�����ڣ���m��4ʱ��S�����ֵ��S���ֵΪ8����E������Ϊ��2��0������BCEΪ���������Σ�
��m��ȡֵ��Χ��0��m��8����3�����ڣ���m��4ʱ��S�����ֵ��S���ֵΪ8����E������Ϊ��2��0������BCEΪ���������Σ�
��������
��1���ⷽ����ã�![]() ���������⣬�õ�
���������⣬�õ�![]() ����Ϊ
����Ϊ![]() ����
����![]() ����Ϊ
����Ϊ![]() ���ɵ�
���ɵ�![]() ����Ϊ
����Ϊ![]() ������������������ʽ�г�����������
������������������ʽ�г�����������![]() ��ֵ���ɣ�
��ֵ���ɣ�
��2���������F��FG��AB������ΪG����![]() ���ó���BEF�ס�BAC���������Ʊ����EF�� sin��FEG��sin��CAB��
���ó���BEF�ס�BAC���������Ʊ����EF�� sin��FEG��sin��CAB��![]() �� S��S��BCES��BFE=
�� S��S��BCES��BFE=![]() �����S��m֮��ĺ�����ϵʽ��
�����S��m֮��ĺ�����ϵʽ��
��3�������䷽������2����S��m֮��ĺ�����ϵʽд������ʽ������S�����ֵʱ��m��ֵ���Ӷ�ȷ����E������͡�BCE����״��
��1������![]() ��������Ϊ2��8.
��������Ϊ2��8.
���ڵ�B��x�������ϣ���C��y���������ϣ���![]() ������
������![]() ��
��![]() ����
����![]() ����
����![]() ����Ϊ
����Ϊ![]() .
.
��Ϊ��![]() ����Ϊ
����Ϊ![]() ������
������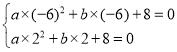
��ã�![]() ��
��![]() .
.
�ʴ˶��κ����ı���ʽΪ![]() .
.
��2����AB��8��OC��8�������⣬AE��m����BE��8m��
��OA��6��OC��8��
��AC��10��
��EF��AC��
���BEF�ס�BAC��
��![]() ��
��
��![]() ��
��
��EF��![]() ��
��
����F��FG��AB������ΪG����sin��FEG��sin��CAB��![]() ��
��
��![]() ��
��
��FG��![]()
![]() ��8m��
��8m��
��S��S��BCES��BFE
��![]() ��8m����8
��8m����8![]() ��8m����8m��
��8m����8m��
��![]() ��8m����88��m��
��8m����88��m��
��![]() ��8m��m
��8m��m
��![]() ���Ա���m��ȡֵ��Χ��0��m��8��
���Ա���m��ȡֵ��Χ��0��m��8��
�ʴ�Ϊ��S��![]() ��m��ȡֵ��Χ��0��m��8��
��m��ȡֵ��Χ��0��m��8��
��3�����ڣ�
�������£�
��S��![]() =
=![]() ��m4��2��8����
��m4��2��8����![]() ��0��
��0��
�൱m��4ʱ��S�����ֵ��S���ֵ��8��
��m��4��
���E��������2��0����
���C���߶�BE�Ĵ�ֱƽ�����ϣ�CE=CB,
���BCE����������
�ʴ�Ϊ�����ڣ�S���ֵ��8��EΪ��2��0������BCEΪ���������Σ�
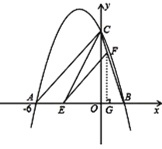

 �����ߴ���ϵ�д�
�����ߴ���ϵ�д�