题目内容
在△ABC中,∠ACB=90°,∠A<45°,点O为AB中点,一个足够大的三角板的直角顶点与点O重合,一边OE经过点C,另一边OD与AC交于点M.
(1)如图1,当∠A=30°时,求证:MC2=AM2+BC2;
(2)如图2,当∠A≠30°时,(1)中的结论是否成立?如果成立,请说明理由;如果不成立,请写出你认为正确的结论,并说明理由;
(3)将三角形ODE绕点O旋转,若直线OD与直线AC相交于点M,直线OE与直线BC相交于点N,连接MN,则MN2=AM2+BN2成立吗?
答: (填“成立”或“不成立”)
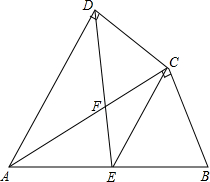
解:(1)证明:如图,过A作AF⊥AC交CO延长线于F,连接MF,
∵∠ACB=90°,∴BC∥AF。∴△BOC∽△AOF。
∴ 。
。
∵O为AB中点,∴OA=OB。∴AF=BC,CO=OF。
∵∠MOC=90°,∴OM是CF的垂直平分线。
∴CM=MF。
在Rt△AMF中,
由勾股定理得:MF2=AM2+AF2=AM2+BC2,
即MC2=AM2+BC2。
(2)还成立。理由如下:
如图,过A作AF⊥AC交CO延长线于F,连接MF,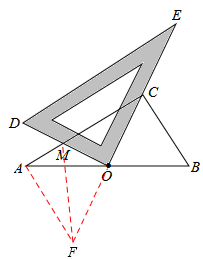
∵∠ACB=90°,∴BC∥AF。∴△BOC∽△AOF。
∴ 。
。
∵OA=OB,∴AF=BC,CO=OF。
∵∠MOC=90°,∴OM是CF的垂直平分线。
∴CM=MF。
在Rt△AMF中,
由勾股定理得:MF2=AM2+AF2=AM2+BC2,
即MC2=AM2+BC2。
(3)成立
解析试题分析:(1)过A作AF⊥AC交CO延长线于F,连接MF,根据相似求出AF=BC,CO=OF,求出FM=CM,根据勾股定理求出即可。
(2)过A作AF⊥AC交CO延长线于F,连接MF,根据相似求出AF=BC,CO=OF,求出FM=CM,根据勾股定理求出即可;
(3)结论依然成立。
如图,以MN的中点P为圆心,MN为直径画圆,则因为∠ACB=90°,∠DOE=90°,所以,根据圆周角定理,O、C在⊙P上。
若MN与AB不平行,设⊙P与AB交于另一点F,
根据割线定理,得 ,
,
∵点O为AB中点,
∴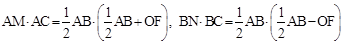 。
。
两式相加,得 ,即
,即 。
。
若MN与AB平行,则易证⊙P与AB相切于点O,
根据切割线定理,得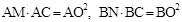 ,即
,即
两式相加,得 ,即
,即 。
。
∴不论MN与AB平行与否,总有 。
。
在Rt△ABC中,由勾股定理得:AB2=AC2+BC2,∴ 。
。
在Rt△MNC中,由勾股定理得:MN2=CM2+CN2,即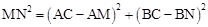 ,
,
∴ 。
。

 ),解答下列问题:
),解答下列问题:
 为何值时,PQ∥BC?
为何值时,PQ∥BC? ),求y与t之间的函数关系式;
),求y与t之间的函数关系式; ,面积是54.求证:AC⊥BD.
,面积是54.求证:AC⊥BD.

 (a≠0,x>0)分别交于D、E两点.
(a≠0,x>0)分别交于D、E两点.
 的值.
的值.


