题目内容
已知:△ABC中,∠B=90°,BE平分∠ABC,AB=6cm,AC=10cm.(1)在BE的延长线上求作一点D,使DA=DC;
(2)四边形ABCD是否有外接圆,并说明理由.若有求外接圆的面积;若没有说明理由.
分析:(1)作边AC的垂直平分线与BE延长线的交点即为D;
(2)要判断四边形ABCD是否有外接圆,只需看能否找到一点到四边形ABCD四个顶点的距离相等,根据直角三角形的性质,知到A、B、C三个顶点距离相等的点是AC的中点,设为H.过A作AM垂直于BE于M,过C作CN垂直于BE于N.设ND长为x,根据CD=AD结合勾股定理列方程(x+
)2+18=x2+32,解方程得x=3
,可以求出CD=5
,故DH可求得为5.因此有外接圆,进一步求得外接圆的面积
(2)要判断四边形ABCD是否有外接圆,只需看能否找到一点到四边形ABCD四个顶点的距离相等,根据直角三角形的性质,知到A、B、C三个顶点距离相等的点是AC的中点,设为H.过A作AM垂直于BE于M,过C作CN垂直于BE于N.设ND长为x,根据CD=AD结合勾股定理列方程(x+
| 2 |
| 2 |
| 2 |
解答:解:(1)作边AC的垂直平分线与BE延长线的交点即为D,如图;
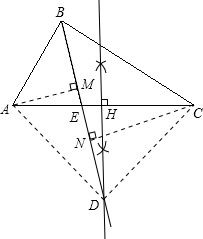
(2)过A作AM⊥BE于M,过C作CN⊥BE于N.则三角形BCN和三角形ABM都是等腰直角三角形,且BC=8cm.
根据等腰直角三角形的性质,得CN=BN=4
cm,AM=BM=3
cm,则MN=
cm.
根据DH是AC的垂直平分线,则AD=CD,设ND长为xcm,根据勾股定理,列方程,得
(x+
)2+18=x2+32,
解得x=3
,
根据勾股定理,得CD=5
,在直角三角形CDH中,根据勾股定理,得DH=5cm,
又根据直角三角形的性质,知H到A、B、C三个顶点距离相等,且该距离是5cm.
因此四边形ABCD是否有外接圆,且外接圆的面积是25πcm2.

(2)过A作AM⊥BE于M,过C作CN⊥BE于N.则三角形BCN和三角形ABM都是等腰直角三角形,且BC=8cm.
根据等腰直角三角形的性质,得CN=BN=4
| 2 |
| 2 |
| 2 |
根据DH是AC的垂直平分线,则AD=CD,设ND长为xcm,根据勾股定理,列方程,得
(x+
| 2 |
解得x=3
| 2 |
根据勾股定理,得CD=5
| 2 |
又根据直角三角形的性质,知H到A、B、C三个顶点距离相等,且该距离是5cm.
因此四边形ABCD是否有外接圆,且外接圆的面积是25πcm2.
点评:此题综合考查了线段垂直平分线的性质、等腰直角三角形的性质、证明几点共圆的方法,即这几个点到某一定点的距离相等.

练习册系列答案
相关题目
 如图所示,已知在△ABC中,AB=AC,∠BAD=β,且AD=AE,求∠EDC.(用β表示)
如图所示,已知在△ABC中,AB=AC,∠BAD=β,且AD=AE,求∠EDC.(用β表示) 8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.
8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个. 外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,
外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,