题目内容
已知Rt△ABC中,∠ACB=90°,BC=5,tan∠A=| 3 |
| 4 |
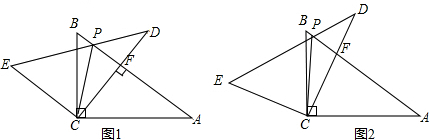
(1)当CD⊥AB时(如图1),求证:PC平分∠EPA;
(2)当点P在边AB上时(如图2),求证:PE+PB=6;
(3)在△ABC旋转过程中,连接BE,当△BCE的面积为
| 25 |
| 4 |
| 3 |
分析:(1)根据旋转前后三角形的面积不变作为相等关系得到CF=CN,从而判定CP平分∠EPA;
(2)作辅助线构造全等三角形,利用全等的性质和三角函数求解.在PA上截取PM=PE连接CM,过C作CK⊥PA得出,CM=CB=5,再利用三角函数求出BM=6,所以得到PM+PE=6;
(3)要注意有2种情况,△BEC为锐角三角形时和△BEC为钝角三角形时两种,不要漏掉.主要利用直角三角形的勾股定理作为等量关系解方程求线段的长度.
(2)作辅助线构造全等三角形,利用全等的性质和三角函数求解.在PA上截取PM=PE连接CM,过C作CK⊥PA得出,CM=CB=5,再利用三角函数求出BM=6,所以得到PM+PE=6;
(3)要注意有2种情况,△BEC为锐角三角形时和△BEC为钝角三角形时两种,不要漏掉.主要利用直角三角形的勾股定理作为等量关系解方程求线段的长度.
解答:解:(1)过C点作CN⊥DE垂足为N,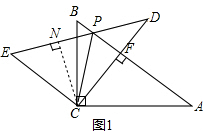
∵△ABC≌△DEC,
∴AB=DE.
∵S△ABC=
AB•CF=S△DCE=
DE•CN,
∵CF=CN,
∴CP平分∠EPA.
(2)如图2在PA上截取PM=PE连接CM,过C作CK⊥PA,
由(1)同理可证CP平分∠EPA,
∴∠EPC=∠APC.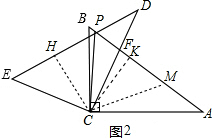
∵PM=PE,PC=PC,
∴△PMC≌△PEC,
∴CE=CM,PE=PM.
又∵CE=CB,
∴CM=CB=5,且CK⊥PA,
∴K为BM的中点,即BK=
BM,
在△BCK中,cos∠B=
=
=
,
在△ABC中,tan∠A=
=
,
∴AC=
.
∵AB=
=
,
∴cos∠B=
=
.
∴BM=6.
∵BM=PM+PB,
∴PE+PB=6.
(3)如图3,∵△BCE的面积为
,BC=5,
∴BE=BC=5,∠CED=∠PBC,∠ECB=60°,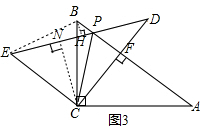
∴∠BPE=60°.
过B点BH⊥PE,设BP=x,
∵PE+BP=6,
∴PE=6-x,PH=
x,BH=
x.
∴52=(
x)2+(6-x-
x)2,x=3±
.
∵3-
<5,
∴∠BPC=120°,
∴BP<BC,
 ∴x=3-
∴x=3-
,
∴BP=3-
.
如图4,当△BEC为钝角三角形时,同理可得BE=5
,PE-PB=6,
∵PE=6+x,∠BPE=60°,x=-3±4
∵-3-4
<0,
∴x=4
-3.
∴BP=3-
或4
-3.

∵△ABC≌△DEC,
∴AB=DE.
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∵CF=CN,
∴CP平分∠EPA.
(2)如图2在PA上截取PM=PE连接CM,过C作CK⊥PA,
由(1)同理可证CP平分∠EPA,
∴∠EPC=∠APC.

∵PM=PE,PC=PC,
∴△PMC≌△PEC,
∴CE=CM,PE=PM.
又∵CE=CB,
∴CM=CB=5,且CK⊥PA,
∴K为BM的中点,即BK=
| 1 |
| 2 |
在△BCK中,cos∠B=
| BK |
| BC |
| ||
| 5 |
| BM |
| 10 |
在△ABC中,tan∠A=
| 3 |
| 4 |
| 5 |
| AC |
∴AC=
| 20 |
| 3 |
∵AB=
52+(
|
| 25 |
| 3 |
∴cos∠B=
| 3 |
| 5 |
| BM |
| 10 |
∴BM=6.
∵BM=PM+PB,
∴PE+PB=6.
(3)如图3,∵△BCE的面积为
| 25 |
| 4 |
| 3 |
∴BE=BC=5,∠CED=∠PBC,∠ECB=60°,

∴∠BPE=60°.
过B点BH⊥PE,设BP=x,
∵PE+BP=6,
∴PE=6-x,PH=
| 1 |
| 2 |
| ||
| 2 |
∴52=(
| ||
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 3 |
∵3-
| 4 |
| 3 |
| 3 |
∴∠BPC=120°,
∴BP<BC,
 ∴x=3-
∴x=3-4
| ||
| 3 |
∴BP=3-
4
| ||
| 3 |
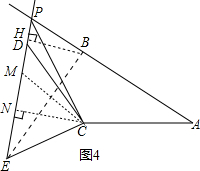
如图4,当△BEC为钝角三角形时,同理可得BE=5
| 3 |
∵PE=6+x,∠BPE=60°,x=-3±4
| 3 |
∵-3-4
| 3 |
∴x=4
| 3 |
∴BP=3-
4
| ||
| 3 |
| 3 |
点评:本题考查旋转相等的性质和解直角三角形的运用,要掌握旋转的性质:对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AB边所在的直线为轴,将△ABC旋转一周,则所得几何体的表面积是( )
如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AB边所在的直线为轴,将△ABC旋转一周,则所得几何体的表面积是( )A、
| ||
| B、24π | ||
C、
| ||
| D、12π |
 22、如图所示,已知Rt△ABC中,AB=AC,BD平分∠ABC,CE⊥BD交BD延长线于E,BA、CE延长线相交于F点.
22、如图所示,已知Rt△ABC中,AB=AC,BD平分∠ABC,CE⊥BD交BD延长线于E,BA、CE延长线相交于F点. 10、如图,已知Rt△ABC中,∠C=90°∠A=36°,以C为圆心,CB为半径的圆交AB于P,则弧BP的度数是
10、如图,已知Rt△ABC中,∠C=90°∠A=36°,以C为圆心,CB为半径的圆交AB于P,则弧BP的度数是 已知Rt△ABC中,∠ACB=90°,CA=CB,点D在BC的延长线上,点E在AC上,且CD=CE,延长BE交AD于点F,求证:BF⊥AD.
已知Rt△ABC中,∠ACB=90°,CA=CB,点D在BC的延长线上,点E在AC上,且CD=CE,延长BE交AD于点F,求证:BF⊥AD.