题目内容
【题目】四边形ABCD为矩形,G是BC上的任意一点,DE⊥AG于点E.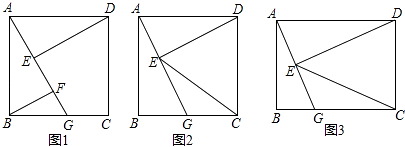
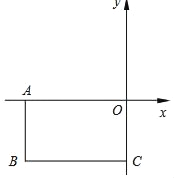
(1)如图1,若AB=BC,BF∥DE,且交AG于点F,求证:AF﹣BF=EF;
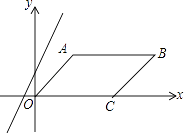
(2)如图2,在(1)条件下,AG= ![]() BG,求
BG,求 ![]() ;
;
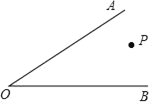
(3)如图3,连EC,若CG=CD,DE=2,GE=1,则CE=(直接写出结果)
【答案】
(1)证明:∵四边形ABCD为矩形,AB=BC,
∴四边形ABCD为正方形,
∴AD=AB,∠BAD=90°,
又DE⊥AG,BF∥DE,
∴∠AED=∠AFB=90°,
∵∠BAF+∠DAE=90°,∠BAE+∠ABF=90°,
∴∠DAE=∠ABF,
在△AED和△BFA中,
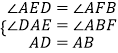
∴△AED≌△BFA(AAS),
∴AE=BF,
∴AF﹣BF=EF,
(2)解:如图2,延长AG与DC交于点F,
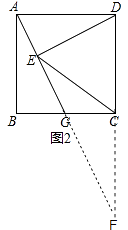
∵AG= ![]() BG,设BG=t,则AG=
BG,设BG=t,则AG= ![]() t,
t,
在Rt△ABG中,AB= ![]() =2t,
=2t,
∴G为BC的中点,
在△ABG和△FCG中,
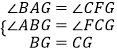
∴△ABG≌△FCG(AAS),
∴AB=FC=CD,
又∵DE⊥AG,
在Rt△DEF中,C为斜边DF的中点,
∴EC=CD=CF,
∴ ![]() =
= ![]() =
= ![]()
(3)![]()
【解析】解:(3)如图3,连接DG,作EM⊥BC于M点,

∵DE⊥AG,DE=2,GE=1,
∴在Rt△DEG中,DG= ![]() =
= ![]() =
= ![]() ,
,
∵CG=CD,
∴在Rt△DCG中,∠CDG=∠CGD=45°,
∴CD=CG= ![]() =
= ![]() ,
,
∵∠BAG+∠GAD=90°,∠EDA+∠GAD=90°,
∴∠BAG=∠EDA,
∵∠ABG=∠DEA=90°,
∴△ABG∽△DEA,
∴ ![]() =
= ![]() ,
,
设AD=x,则AE= ![]() =
= ![]() ,AG=
,AG= ![]() +1,
+1,
∴ ![]() =
= ![]() ,
,
解得x1= ![]() ,x2=﹣2
,x2=﹣2 ![]() (舍去)
(舍去)
∴AE= ![]() =
= ![]() ,
,
又∵∠BAG=∠MEG,
∴∠EDA=∠MEG,
∴△EMG∽△DEA
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]()
解得EM= ![]() ,MG=
,MG= ![]() ,
,
∴CM=CG+MG= ![]() +
+ ![]() =
= ![]() ,
,
∴CE= ![]() =
= ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.

【题目】“PM2.5”指数是空气中可入肺颗粒物的含量,是空气质量的指标之一.下表为A市1﹣12月“PM2.5月平均指数”(单位:微克/立方米)
PM2.5指数 | 20 | 30 | 40 | 41 | 43 | 50 |
月数 | 2 | 4 | 3 | 1 | 1 | 1 |
(1)求这12个月“PM2.5月平均指数”的众数、中位数、平均数;
(2)根据《环境空气质量标准》,宜居城市的标准之一是“PM2.5年平均指数少于35微克/立方米”,请你判断A市是否为宜居城市?