题目内容
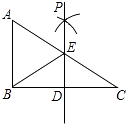
【题目】已知:在![]() 中,
中, ![]() ,
, ![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在线段
在线段![]() 上(点
上(点![]() 不与点
不与点![]() 、
、![]() 重合),且
重合),且![]() .
.
(![]() )如图
)如图![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() __________
__________![]() ,
, ![]() __________
__________![]() .
.
(![]() )如图
)如图![]() ,①求证:
,①求证: ![]() .
.
②若![]() ,且
,且![]() ,求
,求![]() 的度数.
的度数.


【答案】(1)![]() ,
, ![]() ;(2)①见解析;②
;(2)①见解析;②![]()
【解析】试题分析:(1)由等腰三角形的性质得到∠EBC=∠ECB=27°,根据角平分线的性质得到∠DEB=∠EBC+∠ECB=54°,再由角平分线的性质得到∠ACD=∠ECB=27°,因为∠EAC=2∠EBC=54°,求得∠AEC=180°-27°-54°=99°;
(2)在CB上截取CF,使CF=CA,连接EF,构造全等三角形,由全等三角形的性质推出AE=FE,再根据FB=FE,得到AE=FB,即可得出AE+AC=FB+FC=BC;
(3)在CB上截取CF,使CF=CA,连接EF,连接AF,由∠ECB=30°,得到∠ACB=60°,于是推出△AFC是等边三角形,通过三角形全等得到∠EBC=∠FAE,由∠FAC=60°,得到∠EAC=2∠EBC=2∠FAE,于是得出∠EBC的度数.
试题解析:解:(1)∵EB=EC,∴∠EBC=∠ECB=27°,∴∠DEB=∠EBC+∠ECB=54°.
∵CD平分∠ACB,∴∠ACD=∠ECB=27°.
∵∠EAC=2∠EBC=54°,∴∠AEC=180°-27°-54°=99°.
故答案为:54°,99°.
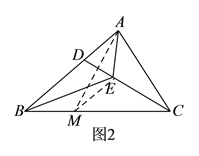
(2)①证明:如图1,在BC上取一点M,使BM=ME,∴∠MBE=∠MEB.
∵∠EAC=2∠MBE,∠EMC=∠MBE+∠MEB=2∠MBE,∴∠EAC=∠EMC.
在△ACE与△MCE中,∵∠CAE=∠CME,∠ACE=∠MCE,CE=CE,∴△ACE≌△MCE(AAS),∴AE=ME, AC =CM,∴AE=BM,∴BC=BM+CM=AE+AC.
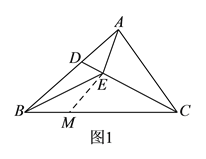
②如图2在BC上取一点M,使BM=ME,连接AM.
∵∠ECB=30°,∴∠ACB=60°,由①可知,△AMC是等边三角形(M点与B点重合),∴AM=AC=BE.
在△EMB与△MEA中,∵AE=BM,EM=EM,AM=BE,∴△EMB≌△MEA,∴∠EBC=∠MAE.
∵∠MAC=60°,∠EAC=2∠EBC=2∠MAE,∴∠MAE=20°,∠EAC=40°,∴∠EBC=20°.

 阅读快车系列答案
阅读快车系列答案