题目内容
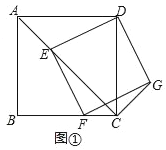
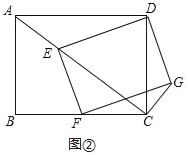
【题目】如图，将一张矩形纸片ABCD沿着对角线BD向上折叠，顶点C落到点E处，BE交AD于点F．过点D作DG∥BE，交BC于点G，连接FG交BD于点O．若AB＝6，AD＝8，则DG的长为_____．
【答案】
【解析】
根据折叠的性质求出四边形BFDG是菱形，假设DF＝BF＝x，∴AF＝AD﹣DF＝8﹣x，根据在直角△ABF中，AB2+AF2＝BF2，即可求解.
解：∵四边形ABCD是矩形，
∴AD∥BC，∴∠ADB=∠DBC
∴FD∥BG，
又∵DG∥BE，
∴四边形BFDG是平行四边形，
∵折叠，∴∠DBC=∠DBF，
故∠ADB =∠DBF
∴DF＝BF，
∴四边形BFDG是菱形；
∵AB＝6，AD＝8，
∴BD＝10．
∴OB＝
BD＝5．
假设DF＝BF＝x，∴AF＝AD﹣DF＝8﹣x．
∴在直角△ABF中，AB2+AF2＝BF2，即62+（8﹣x）2＝x2，
解得x＝，
即DG＝BF＝，
故答案为：
练习册系列答案
名师金手指领衔课时系列答案
相关题目
【题目】某学校组织了“热爱宪法，捍卫宪法”的知识竞赛，赛后发现所有学生的成绩（总分100分）均不低于50分，为了解本次竞赛的成绩分布情况，随机抽取若干名学生的成绩作为样本进行整理，并绘制了不完整的统计图表，请你根据统计图表解答下列问题．
学校若干名学生成绩分布统计表
分数段（成绩为x分） | 频数 | 频率 |
50≤x＜60 | 16 | 0.08 |
60≤x＜70 | a | 0.31 |
70≤x＜80 | 72 | 0.36 |
80≤x＜90 | c | d |
90≤x≤100 | 12 | b |
（1）此次抽样调查的样本容量是 ；
（2）写出表中的a＝ ，b＝ ，c＝ ；
（3）补全学生成绩分布直方图；
（4）比赛按照分数由高到低共设置一、二、三等奖，若有25%的参赛学生能获得一等奖，则一等奖的分数线是多少？
