Question

某种产品的年产量不超过1000吨，该产品的年产量（单位：吨）与费用（单位：万元）之间函数的图象是顶点在原点的抛物线的一部分（如图1）；该产品的年销售量（单位：吨）与销售单价（单位：万元/吨）之间函数的图象是线段（如图2），若生产出的产品都能在当年销售完，则年产量是多少吨时，所获毛利润最大，最大利润是多少（毛利润=销售额-费用）．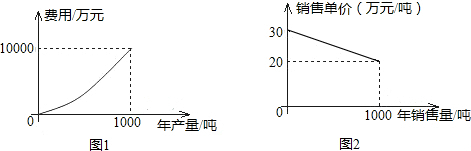

Answer 1

设年产量为x吨，费用为y（万元），销售单价为z（万元），则0≤x≤1000，
由图（1）知将点（1000，10000）代入到y=ax²可求得y=

1

100

x²，
由图（2）求得z=-

1

100

x+30，
设毛利润为w（万元），
则w=xz-y=x（-

1

100

x+30）-

1

100

x²=-

1

50

（x-750）²+11250．
答：年产量是750吨时，所获毛利润最大，为11250万元．