题目内容
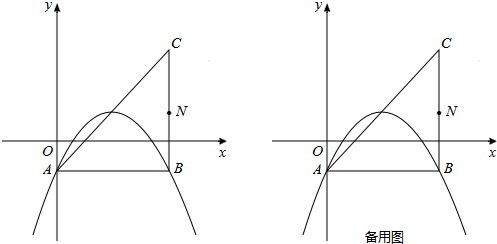
在平面直角坐标系中,已知抛物线y=-
x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,-1),C的坐标为(4,3),直角顶点B在第四象限.
(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;
(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q.
(i)若点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M、P、Q三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M的坐标;
(ii)取BC的中点N,连接NP,BQ.试探究
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
| 1 |
| 2 |
(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;
(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q.
(i)若点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M、P、Q三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M的坐标;
(ii)取BC的中点N,连接NP,BQ.试探究
| PQ |
| NP+BQ |

(1)∵等腰直角三角形ABC的顶点A的坐标为(0,-1),C的坐标为(4,3)
∴点B的坐标为(4,-1).
∵抛物线过A(0,-1),B(4,-1)两点,
∴
,解得:b=2,c=-1,
∴抛物线的函数表达式为:y=-
x2+2x-1.
(2)i)∵A(0,-1),C(4,3),
∴直线AC的解析式为:y=x-1.
设平移前抛物线的顶点为P0,则由(1)可得P0的坐标为(2,1),且P0在直线AC上.
∵点P在直线AC上滑动,∴可设P的坐标为(m,m-1),
则平移后抛物线的函数表达式为:y=-
(x-m)2+m-1.
解方程组:
,
解得
,
∴P(m,m-1),Q(m-2,m-3).
过点P作PE∥x轴,过点Q作QF∥y轴,则
PE=m-(m-2)=2,QF=(m-1)-(m-3)=2.
∴PQ=2
=AP0.
若以M、P、Q三点为顶点的等腰直角三角形,则可分为以下两种情况:
①当PQ为直角边时:点M到PQ的距离为2
(即为PQ的长).
由A(0,-1),B(4,-1),P0(2,1)可知,
△ABP0为等腰直角三角形,且BP0⊥AC,BP0=2
.
如答图1,过点B作直线l1∥AC,交抛物线y=-
x2+2x-1于点M,则M为符合条件的点.
∴可设直线l1的解析式为:y=x+b1,
∵B(4,-1),∴-1=4+b1,解得b1=-5,
∴直线l1的解析式为:y=x-5.
解方程组
,得:
,
∴M1(4,-1),M2(-2,-7).

②当PQ为斜边时:MP=MQ=2,可求得点M到PQ的距离为
.
如答图2,取AB的中点F,则点F的坐标为(2,-1).
由A(0,-1),F(2,-1),P0(2,1)可知:
△AFP0为等腰直角三角形,且点F到直线AC的距离为
.
过点F作直线l2∥AC,交抛物线y=-
x2+2x-1于点M,则M为符合条件的点.
∴可设直线l2的解析式为:y=x+b2,
∵F(2,-1),∴-1=2+b2,解得b2=-3,
∴直线l2的解析式为:y=x-3.
解方程组
,得:
,
∴M3(1+
,-2+
),M4(1-
,-2-
).
综上所述,所有符合条件的点M的坐标为:
M1(4,-1),M2(-2,-7),M3(1+
,-2+
),M4(1-
,-2-
).
ii)
存在最大值.理由如下:
由i)知PQ=2
为定值,则当NP+BQ取最小值时,
有最大值.
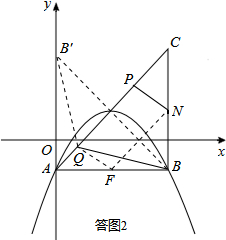
如答图2,取点B关于AC的对称点B′,易得点B′的坐标为(0,3),BQ=B′Q.
连接QF,FN,QB′,易得FN∥PQ,且FN=PQ,
∴四边形PQFN为平行四边形.
∴NP=FQ.
∴NP+BQ=FQ+B′Q≥FB′=
=2
.
∴当B′、Q、F三点共线时,NP+BQ最小,最小值为2
.
∴
的最大值为
=
.
∴点B的坐标为(4,-1).
∵抛物线过A(0,-1),B(4,-1)两点,
∴
|
∴抛物线的函数表达式为:y=-
| 1 |
| 2 |
(2)i)∵A(0,-1),C(4,3),
∴直线AC的解析式为:y=x-1.
设平移前抛物线的顶点为P0,则由(1)可得P0的坐标为(2,1),且P0在直线AC上.
∵点P在直线AC上滑动,∴可设P的坐标为(m,m-1),
则平移后抛物线的函数表达式为:y=-
| 1 |
| 2 |
解方程组:
|
解得
|
|
∴P(m,m-1),Q(m-2,m-3).
过点P作PE∥x轴,过点Q作QF∥y轴,则
PE=m-(m-2)=2,QF=(m-1)-(m-3)=2.
∴PQ=2
| 2 |
若以M、P、Q三点为顶点的等腰直角三角形,则可分为以下两种情况:
①当PQ为直角边时:点M到PQ的距离为2
| 2 |
由A(0,-1),B(4,-1),P0(2,1)可知,
△ABP0为等腰直角三角形,且BP0⊥AC,BP0=2
| 2 |
如答图1,过点B作直线l1∥AC,交抛物线y=-
| 1 |
| 2 |
∴可设直线l1的解析式为:y=x+b1,
∵B(4,-1),∴-1=4+b1,解得b1=-5,
∴直线l1的解析式为:y=x-5.
解方程组
|
|
|
∴M1(4,-1),M2(-2,-7).

②当PQ为斜边时:MP=MQ=2,可求得点M到PQ的距离为
| 2 |
如答图2,取AB的中点F,则点F的坐标为(2,-1).
由A(0,-1),F(2,-1),P0(2,1)可知:
△AFP0为等腰直角三角形,且点F到直线AC的距离为
| 2 |
过点F作直线l2∥AC,交抛物线y=-
| 1 |
| 2 |
∴可设直线l2的解析式为:y=x+b2,
∵F(2,-1),∴-1=2+b2,解得b2=-3,
∴直线l2的解析式为:y=x-3.
解方程组
|
|
|
∴M3(1+
| 5 |
| 5 |
| 5 |
| 5 |
综上所述,所有符合条件的点M的坐标为:
M1(4,-1),M2(-2,-7),M3(1+
| 5 |
| 5 |
| 5 |
| 5 |
ii)
| PQ |
| NP+BQ |
由i)知PQ=2
| 2 |
| PQ |
| NP+BQ |

如答图2,取点B关于AC的对称点B′,易得点B′的坐标为(0,3),BQ=B′Q.
连接QF,FN,QB′,易得FN∥PQ,且FN=PQ,
∴四边形PQFN为平行四边形.
∴NP=FQ.
∴NP+BQ=FQ+B′Q≥FB′=
| 22+42 |
| 5 |
∴当B′、Q、F三点共线时,NP+BQ最小,最小值为2
| 5 |
∴
| PQ |
| NP+BQ |
2
| ||
2
|
| ||
| 5 |

练习册系列答案
相关题目
 顶点的三角形与以D,E,F为顶点的三角形全等,求a,b的值.(只需写出结果,不必写出解答过程)
顶点的三角形与以D,E,F为顶点的三角形全等,求a,b的值.(只需写出结果,不必写出解答过程) ,求证:这个二次函数图象的对称轴是x=3.
,求证:这个二次函数图象的对称轴是x=3.