��Ŀ����
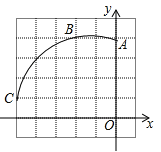
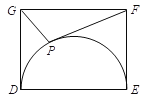
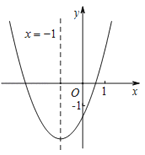
����Ŀ�����κ���y��ax2+bx+c��a��0����ͼ����ͼ��ʾ����Գ���Ϊֱ��x����1����x��Ľ���Ϊ��x1��0������x2��0��������0��x1��1�������н��ۣ���abc��0���ک�3��x2����2����4a��2b+c����1���ܵ�mΪ����ʵ��ʱ��a��b��am2+bm�������㣨��0.5��y1��������2��y2�������������ϣ���y1��y2����a��![]() �����У���ȷ���۵ĸ���Ϊ��������
�����У���ȷ���۵ĸ���Ϊ��������
A.2B.3C.4D.5
���𰸡�B
��������
�ٶԳ�����y����࣬�����ж�ab��0������ͼ����y��Ľ�������ж�c��0�������ж������ڶԳ���Ϊֱ��x=-1��0<x1<1��������⣻
�۶Գ���Ϊֱ��x=-1����b=2a��������⣻
����x=-1�����������Сֵ�������ж���
�ݸ���x=-0.5��x=-2��Գ����Զ�������ж���
����x=1ʱ��y=a+b+c=3a+c>0����3a>-c���������.
�⣺�ٶԳ�����y����࣬����![]() ����ab��0���ɺ���ͼ����y�Ḻ�����ཻ����c<o����abc <0���ʴ���
����ab��0���ɺ���ͼ����y�Ḻ�����ཻ����c<o����abc <0���ʴ���
�ڶԳ���Ϊֱ��x=-1��0<x1<1����-3<x2<-2����ȷ��
�۶Գ���Ϊֱ��x=-1����b=2a��4a-2b+c=c<-1������ȷ��
��x=-1ʱ��y=ax2+bx+c=a-b+c��Ϊ�ú�������Сֵ����a-b+c��am2+bm+c���ʴ���
����x=-0.5�ͶԳ���ľ���Ϊ0.5��x=-2�ͶԳ���ľ���Ϊ1���ɺ���ͼ��ɵ�y1��y2���ʴ���
��x=1ʱ��y=a+b+c=3a+c>0����3a>-c����c<-1����a>![]() ����ȷ��
����ȷ��
�ʴ�ΪB.