题目内容
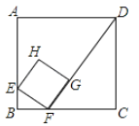
【题目】如图,边长12的正方形ABCD中,F为BC上一点,有一个小正方形EFGH,其中E、G分别在AB、FD上.若BF=3,则AH的长为____.
【答案】![]()
【解析】
由在边长为12的正方形ABCD中,有一个小正方形EFGH,根据同角的余角相等,可得∠BFE=∠CDF,继而证得△BEF∽△CFD,然后由相似三角形的对应边成比例,求得BE长,过H作HM⊥AB于M,则∠HMA=∠HME=90°,求出MH和AM长,再根据勾股定理求出即可.
四边形ABCD是正方形,
∴∠B=∠C=90°,
在△BEF与△CFD中,
∵∠BFE+∠CFD=∠CFD+∠CDF=90°,
∴∠BFE=∠CDF,
∴△BEF∽△CFD,
∴![]() =
=![]() ,
,
∵BF=3,BC=12,
∴CF=BC-BF=12-3=9,
∴![]() =
=![]() ,
,
∴BE=![]() ,
,
过H作HM⊥AB于M,
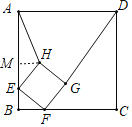
则∠HMA=∠HME=90°,
∵四边形ABCD和四边形EHGF是正方形,
∴∠HME=∠B=90°,EH=EF,∠HEF=90°,
∴∠MEH+∠BEF=90°,∠BEF+∠EFB=90°,
∴∠MEH=∠EFB,
在△HME和△EBF中,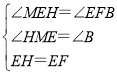 ,
,
∴△HME≌△EBF(AAS),
∴HM=BE=![]() ,ME=BF=3,
,ME=BF=3,
∴AM=AB-EM-BE=12-3-![]() =
=![]() ,
,
在Rt△AMH中,由勾股定理得:AH=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目