题目内容
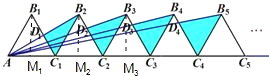
【题目】如图,(n+1)个边长为2的等边三角形有一条边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△B(n+1)DnCn的面积为Sn,则Sn=____(用含n的式子表示).

【答案】![]() .
.
【解析】
试题分析:由于各三角形为等边三角形,且各边长为2,过各三角形的顶点B1、B2、B3…向对边作垂线,垂足为M1、M2、M3,∵△AB1C1是等边三角形,∴AD1=AC1sin60°=2×![]() =
=![]() ,∵△B1C1B2也是等边三角形,∴C1B1是∠AC1B2的角平分线,∴AD1=B2D1=
,∵△B1C1B2也是等边三角形,∴C1B1是∠AC1B2的角平分线,∴AD1=B2D1=![]() ,故S1=S△B2C1A﹣S△AC1D1=
,故S1=S△B2C1A﹣S△AC1D1=![]() =
=![]() ;S2=S△B3C2A﹣S△AC2D2=
;S2=S△B3C2A﹣S△AC2D2=![]() =
=![]() =
=![]() ;
;
作AB∥B1C1,使AB=AB1,连接BB1,则B2,B3,…Bn在一条直线上.
∵Bn Cn∥AB,∴![]() =
=![]() ,∴BnDn=
,∴BnDn=![]() AB=
AB=![]() ,则DnCn=2﹣BnDn=2﹣
,则DnCn=2﹣BnDn=2﹣![]() =
=![]() .
.
△BnCnBn+1是边长是2的等边三角形,因而面积是:![]() .
.
△Bn+1DnCn面积为Sn=![]() =
=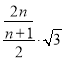 =
=![]() .
.
即第n个图形的面积Sn=![]() .故答案为:
.故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

