��Ŀ����
����Ŀ��ij��λΪ�˴�������������λ�����ڵ�λ��ǽ���߶�MN��ʾ�����һ�������ε��ϵؽ����̻���������ǽ��������Ҫ��դ��Χ�������ƻ���դ��50�ף���AB�ij�Ϊx�ף������ε����Ϊyƽ���ף�
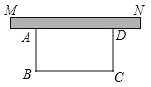
��1�������y��x�ĺ�����ϵʽ������д���Ա�����ȡֵ��Χ��
��2��������ǽ�峤�ȣ���AB�ij�Ϊ����ʱ�������ε�������
��3����ǽ�峤��Ϊ20�ף��ʳ������������Ƕ��٣�
���𰸡���1��y����2x2+50x����2��������ǽ�峤�ȣ�AB�ij�Ϊ12.5��ʱ�������ε�������3����ǽ�峤��Ϊ20�ף���������������300ƽ���ף�
��������
��1�����ݳ����ε�������ڳ����Կ��������![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2����![]() ��
��![]() �ĺ�����ϵʽ�䷽��д�ɶ���ʽ�����ݶ��κ��������ʼ��ɵý⣻
�ĺ�����ϵʽ�䷽��д�ɶ���ʽ�����ݶ��κ��������ʼ��ɵý⣻
��3�����ݶ��κ��������ʼ�ǽ�峤��Ϊ20�ף��ɵó�����������ʱ��![]() ֵ���Ӷ����ó����Կ����ɵô𰸣�
ֵ���Ӷ����ó����Կ����ɵô𰸣�
�⣺��1��![]()
![]() ��
��![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��![]() ��
��
��2��![]()
![]()
![]() ������ϵ��Ϊ
������ϵ��Ϊ![]()
![]() ��
��![]() �ף���
�ף���![]() ��ʱ�������ε�������
��ʱ�������ε�������
![]() ������ǽ�峤�ȣ�
������ǽ�峤�ȣ�![]() �ij�Ϊ12.5��ʱ�������ε�������
�ij�Ϊ12.5��ʱ�������ε�������
��3����![]() ��
��
��![]()
![]()
![]() ������ϵ��Ϊ
������ϵ��Ϊ![]() ���Գ���Ϊ
���Գ���Ϊ![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��![]() �����������
�����������
![]()
![]() ʱ��
ʱ�� ![]() ������������
������������
������Ϊ��![]() ƽ����
ƽ����
![]() ��ǽ�峤��Ϊ20�ף���������������300ƽ���ף�
��ǽ�峤��Ϊ20�ף���������������300ƽ���ף�

 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�