Question

【题目】抛物线的顶点为（m，n）抛物线的顶点为（m,n），如果 ，那么我们称抛物线与关于点 中心对称，给出抛物线①；②

(1)判断抛物线①与抛物线②是否中心对称?若是，求出对称中心的坐标；若不是，说明理由；

(2)直线y=m交抛物线①于A. B两点，交抛物线②于C. D两点，如果AB=2CD，求m的值；

(3)设抛物线①与抛物线②的顶点分别为M、N，点P在x轴上移动，若△MNP为直角三角形，求点P坐标。

Answer 1

【答案】(1) (2) (3)见解析

【解析】

（1）根据二次函数解析式，求出两函数的关系，结合顶点坐标得出对称中心；

（2）利用根与系数的关系以及两点之间的距离得出m的值即可；

（3）利用勾股定理得出符合要求的所有点的坐标．

(1)抛物线①的 =1,

抛物线②的=1.

∵，

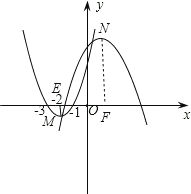
∴抛物线①与抛物线②是中心对称,抛物线①的顶点坐标(2,1)，

抛物线②的顶点坐标(2,5)，

∴对称中心的坐标 ，即：(0,2)；

(2)点A. B的横坐标是方程x+4x+3=m的两根，

∴x+x=4, x.x=3m，

∴AB=| x-x|=

同理CD=，

∵AB=2CD，

解得：m=；

(3)设点P(n,0).由(1)得M(2,1),N(2,5)，

作ME⊥x轴于E,作NF⊥x轴于F,PN=NF+PF=25+(n2) ，

同理PM=ME+PE=1+(n+2),MN=4+6=52.

若∠MNP=90,PM=MN+PN,解得n=；

若∠NMP=90,PN=MN+PM,解得n=；

若∠NPM=90,PN+PM=MN,解得n=±3

综上,点P坐标为：P(192,0),P(72,0),P(3,0),P(3,0).