Question

【题目】已知抛物线y＝ax2+（1﹣2a）x+c（a，c是常数，且a≠0），过点（0，2）．

（1）求c的值，并通过计算说明点（2，4）是否也在该抛物线上；

（2）若该抛物线与直线y＝5只有一个交点，求a的值；

（3）若当0≤x≤2时，y随x的增大而增大，求a的取值范围．

Answer 1

【答案】（1）c＝2，说明见解析；（2）a的值是或；（3）﹣≤a＜0．

【解析】

（1）根据抛物线y＝ax2+（1﹣2a）x+c（a，c是常数，且a≠0），过点（0，2），可以得到c的值，然后将x＝2代入抛物线解析式，即可得到y的值，从而可以判断点（2，4）是否也在该抛物线上；

（2）根据该抛物线与直线y＝5只有一个交点，可知该抛物线顶点的纵坐标是5，从而可以求得a的值；

（3）根据当0≤x≤2时，y随x的增大而增大，可知a＜0，该抛物线的对称轴≥2，从而可以求得a的取值范围．

解：（1）∵抛物线y＝ax2+（1﹣2a）x+c（a，c是常数，且a≠0），过点（0，2），

∴c＝2，

∴抛物线y＝ax2+（1﹣2a）x+2，

当x＝2时，

y＝4a+2（1﹣2a）+2＝4a+2﹣4a+2＝4，

即点（2，4）在该抛物线上；

（2）∵抛物线y＝ax2+（1﹣2a）x+2，该抛物线与直线y＝5只有一个交点，

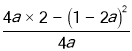∴＝5，

解得，a＝，

即a的值是或；

（3）∵当0≤x≤2时，y随x的增大而增大，抛物线y＝ax2+（1﹣2a）x+2，

∴a＜0，≥2，

解得，a，

即a的取值范围是﹣≤a＜0．