题目内容
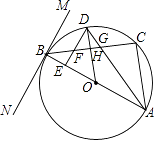
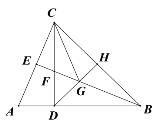
【题目】如图,在△ABC中,AB=BC,CD⊥AB于点D,CD=BD.BE平分∠ABC,点H是BC边的中点.连接DH,交BE于点G.连接CG.
(1)求证:△ADC≌△FDB;
(2)求证:![]()
(3)判断△ECG的形状,并证明你的结论.
【答案】(1)见解析;(2)见解析;(3)△ECG为等腰直角三角形,理由见解析.
【解析】
(1)首先根据AB=BC,BE平分∠ABC,得到BE⊥AC,CE=AE,进一步得到∠ACD=∠DBF,结合CD=BD,即可证明出△ADC≌△FDB;
(2)由△ADC≌△FDB得到AC=BF,结合CE=AE,即可证明出结论;
(3)由点H是BC边的中点,得到GH垂直平分BC,即GC=GB,由∠DBF=∠GBC=∠GCB=∠ECF,得∠ECO=45°,结合BE⊥AC,即可判断出△ECG的形状.
(1)∵AB=BC,BE平分∠ABC
∴BE⊥AC
∵CD⊥AB
∴∠ACD=∠ABE(同角的余角相等)
又∵CD=BD
∴△ADC≌△FDB
(2)∵AB=BC,BE平分∠ABC
∴AE=CE
则CE=![]() AC
AC
由(1)知:△ADC≌△FDB
∴AC=BF
∴CE=![]() BF
BF
(3)△ECG为等腰直角三角形,理由如下:
由点H是BC的中点,得GH垂直平分BC,从而有CG=BG,
则∠EGC=2∠CBG=∠ABC=45°,
又∵BE⊥AC,
故△ECG为等腰直角三角形.

练习册系列答案
相关题目