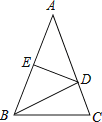题目内容
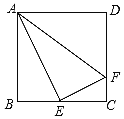
【题目】如图，在正方形ABCD中，E是BC的中点，F是CD上一点，且CF＝
CD，下列结论中错误的是（ ）
A.
B.△ABE∽△AEF
C.△ABE∽△ECFD.△ADF∽△ECF
【答案】D
【解析】
推导出∠B=∠C=90°，AB：EC=BE：CF=2：1，从而△ABE∽△ECF，故EF=
AE，进而∠AEF=∠B=90°，由此能得到△ABE∽△AEF，AE⊥EF．
解：∵在正方形ABCD中，E是BC的中点，F是CD上一点，且CF＝
CD，
∴∠B＝∠C＝90°，AB：EC＝BE：CF＝2：1．
∴△ABE∽△ECF．
∴AB：EC＝AE：EF＝2：1，∠AEB＝∠EFC．
∵BE＝CE，∠FEC+∠EFC＝90°，
∴AB：AE＝BE：EF，∠AEB+∠FEC＝90°．
∴∠AEF＝∠B＝90°．
∴△ABE∽△AEF．
∴A，B，C正确．
在△ADF和△ECF中，两直角边的对应比不相等，故△ADF和△ECF不相似.
故选：D．
练习册系列答案
相关题目
【题目】某公司销售部有营业员15人，该公司为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对营业员进行适当的奖励，为了确定一个适当的月销售目标，公司有关部门统计了这15人某月的销售量，如下表所示：
月销售量/件数 | 1770 | 480 | 220 | 180 | 120 | 90 |
人数 | 1 | 1 | 3 | 3 | 3 | 4 |
(1)直接写出这15名营业员该月销售量数据的平均数、中位数、众数；
(2)如果想让一半左右的营业员都能达到月销售目标，你认为(1)中的平均数、中位数、众数中，哪个最适合作为月销售目标？请说明理由.
