��Ŀ����
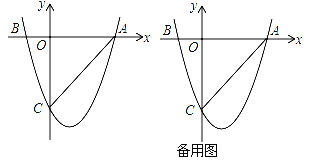
����Ŀ����ͼ�����κ���y=ax2+bx+c��a��0����ͼ����x�ύ��A��3��0����B����1��0����������y���ཻ�ڵ�C��0����3��
��1����ö��κ����Ľ���ʽ��
��2����E��y���Ҳ������������ڵ�A��һ������������E��x���ƽ���߽�����������һ��F������F��FG��ֱ��x���ڵ�G���ٹ���E��EH��ֱ��x���ڵ�H���õ�����EFGH�����ڵ�E���˶���������������EFGHΪ������ʱ������������εı߳���
��3����P����x���·����������ϵ�һ������������PA��PC������PAC�����ȡֵ��Χ������PAC���Ϊ����ʱ����������PAC�м�����
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() ����5����
����5����
�������������������1���轻��ʽΪy=a��x+1����x-3����Ȼ���C������������a���ɣ�
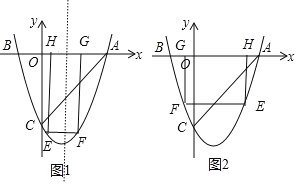
��2����E��t��t2-2t-3�������ۣ���0<t<1ʱ����ͼ1��EF=2��1-t����EH=-��t2-2t-3�������������ε����ʵ�2��1-t��=-��t2-2t-3������1<t<3ʱ����ͼ2�����������ε����ʵ�2��t-1��=-��t2-2t-3������t>3ʱ��2��t-1��=t2-2t-3��Ȼ��ֱ�ⷽ�̵õ�����������t��ֵ���ټ������Ӧ�������εı߳���
��3����P��x��x2-2x-3�������ۣ���-1<x<0ʱ������S��ABC=6����0<S��APC<6����0<x<3ʱ����PM��y�ύAC�ڵ�M����ͼ3�����ֱ��AC�Ľ���ʽΪy=x-3����M��x��x-3�������������������ʽ��S��APC=![]() 3��-x2+3x�������ö��κ��������ʵ�0<S��APC<
3��-x2+3x�������ö��κ��������ʵ�0<S��APC<![]() ������0<S��APC<6�����ǵõ���PAC���Ϊ����ʱ������ֵΪ1��2��3��4��5��
������0<S��APC<6�����ǵõ���PAC���Ϊ����ʱ������ֵΪ1��2��3��4��5��
���������(1)�������߽���ʽΪy=a(x+1)(x3)��
��C(0,3)�����3a=3�����a=1��
���������߽���ʽΪy=(x+1)(x3)��
��y=x22x3��
(2)�����ߵĶԳ���Ϊֱ��x=1��
��E(t,t22t3)��
��0<t<1ʱ,��ͼ1,EF=2(1t),EH=(t22t3)��
�߾���EFGHΪ�����Σ�
��EF=EH,��2(1t)=(t22t3)��
������t24t1=0,���t1=2+![]() (��ȥ),t2=2
(��ȥ),t2=2![]() (��ȥ)��
(��ȥ)��
��1<t<3ʱ,��ͼ2,EF=2(t1),EH=(t22t3)��
�߾���EFGHΪ�����Σ�
��EF=EH,��2(t1)=(t22t3)��
������t25=0,���t1=![]() ,t2=
,t2=![]() (��ȥ)��
(��ȥ)��
��ʱ������EFGH�ı߳�Ϊ2![]() 2��
2��
��t>3ʱ,EF=2(t1),EH=t22t3,
�߾���EFGHΪ�����Σ�
��EF=EH,��2(t1)=t22t3��
������t24t1=0,���t1=2+![]() ,t2=2
,t2=2![]() (��ȥ)��
(��ȥ)��
��ʱ������EFGH�ı߳�Ϊ2![]() +2��
+2��
��������������EFGH�ı߳�Ϊ2![]() 2��2
2��2![]() +2��
+2��
(3)��P(x,x22x3)��
��1<x<0ʱ��
��S��ABC=![]() ��4��3=6��
��4��3=6��
��0<S��APC<6��
��0<x<3ʱ,��PM��y�ύAC�ڵ�M����ͼ3��
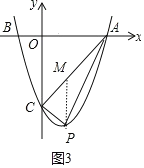
��ֱ��AC�Ľ���ʽΪy=x3,��M(x,x3)��
��PM=x3(x22x3)=x2+3x��
��S��APC=![]() ��3(x2+3x)=
��3(x2+3x)=![]() x2+
x2+![]() x=
x=![]() (x
(x![]() )2+
)2+![]() ��
��
��x=![]() ʱ,S��APC����������ֵΪ
ʱ,S��APC����������ֵΪ![]() ,��0<S��APC<
,��0<S��APC<![]() ��
��
��������,0<S��APC<6��
���PAC���Ϊ����ʱ������ֵΪ1��2��3��4��5������PAC��5��.

 �������ͬ����ϰϵ�д�
�������ͬ����ϰϵ�д�