��Ŀ����
����Ŀ��ijˮ������������ÿ�����Ϊ40Ԫ�ĸ��٣���۲��Ź涨ÿ���ۼ۲��ø���55Ԫ���г����鷢�֣���ÿ����45Ԫ�ļ۸����ۣ�ƽ��ÿ������105�䣻ÿ����50Ԫ�ļ۸����ۣ�ƽ��ÿ������90�䣮�ٶ�ÿ��������y���䣩�����ۼ�x��Ԫ/�䣩֮������һ�κ�����ϵʽ��
��1����ƽ��ÿ��������y���䣩�����ۼ�x��Ԫ/�䣩֮��ĺ�����ϵʽ��
��2�����������ƽ��ÿ�����������w��Ԫ�������ۼ�x��Ԫ/�䣩֮��ĺ�����ϵʽ��
��3����ÿ��ƻ�������ۼ�Ϊ����Ԫʱ�����Ի�����������������Ƕ��٣�
���𰸡�(1)��y����3x��240;��2��w����3 x2��360x��9600;��3�� ��ÿ��ƻ�������ۼ�Ϊ55Ԫʱ�����Ի���������Ϊ1125Ԫ.
��������
��1������ÿ��������y���䣩�����ۼ�x��Ԫ/�䣩֮������һ�κ�����ϵʽ�����ô���ϵ�������һ�κ�������ʽ���ɣ�
��2�����ø�������ƽ��ÿ�����������w��Ԫ��=ÿ�������������ÿ����������ó����ɣ�
��3�����������������Ա�����ȡֵ�õ����ε���ֵ���⼴�ɣ�
��1����y=kx+b��
����֪��45��105������50��90������ã�
![]() ��
��
��ã�![]() ��
��
��ƽ��ÿ��������y���䣩�����ۼ�x��Ԫ/�䣩֮��ĺ�����ϵʽΪ��y=-3x+240��
��2����ˮ������������ÿ�����Ϊ40Ԫ��ƻ�������ۼ�xԪ/�䣬
���������ƽ��ÿ�����������w��Ԫ�������ۼ�x��Ԫ/�䣩֮��ĺ�����ϵʽΪ��
W=��x-40����-3x+240��=-3x2+360x-9600��
��3��W=-3x2+360x-9600=-3��x-60��2+1200��
��a=-3��0���������߿������£�
�֡߶Գ���Ϊx=60���൱x��60��W��x�����������
����50��x��55���൱x=55ʱ��W�����ֵΪ1125Ԫ��
�൱ÿ��ƻ�������ۼ�Ϊ55Ԫʱ�����Ի���������Ϊ1125Ԫ��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
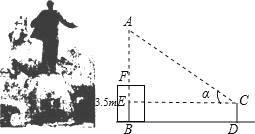
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ũ��ʦʯ������ij��ѧ������1�����ѧ������һ����ѧ����У������������㳡�����������ڹ㳡���ĵ�������ͭ��߶ȣ���֪ͭ������ĸ�Ϊ3.5m��ijС���ʵϰ������������������ͭ��ĸߣ������ȷ��0.1m��
ʵϰ����2003��9��25��
��Ŀ1 | �����ײ����Ե����ͭ��� | |||
| ||||
�� �� �� �� | ������Ŀ | ��һ�� | �ڶ��� | ƽ��ֵ |
BD�ij� | 12.3m | 11.7m | ||
������CD�ĸ� | 1.32m | 1.28m | ||
��� | ��=30��56' | ��=31��4' | ||
�� �� | ||||
��� | ||||