Question

【题目】作出函数的图象，并利用图象回答问题：

(1)写出图象与轴的交点A的坐标________，与轴的交点B的坐标________.

(2)当时，的取值范围是______________.

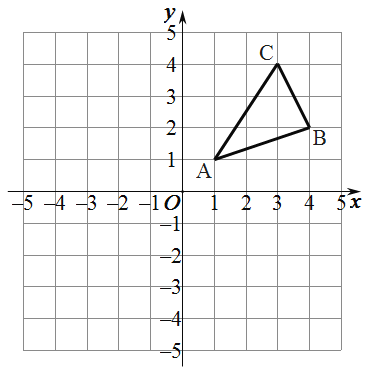
(3)有一点C的坐标是(3，4)，顺次连接点A、B、C得到△ABC，三角形ABC的面积为________.

(4)点C关于轴对称的点D的坐标

(5)连接B，D两点，求直线BD的函数关系式.

Answer 1

【答案】画图见解析；（1）A（2,0），B（0,2）；（2）y<3；（3）5；（4）(3，-4)；（5）y=-2x+2

【解析】

求出函数与x轴和y轴的交点坐标即可作出函数图像；

（1）由图像的画法即可解答；

（2）求出x=-1时y的值，结合图形解答即可；

（3）用割补法求解即可；

（4）根据关于x轴对称的点横坐标不变，纵坐标互为相反数求解即可；

（5）用待定系数法求解即可.

解：当x=0时， =0,

当y=0时，0=-x+2，即x=2.

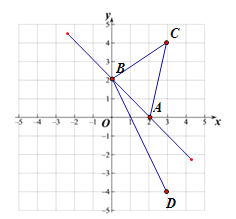
（1）图象与轴的交点A的坐标（2,0），与轴的交点B的坐标（0,2）；

（2）∵当x=-1时，y=1+2=3,

∴当时，的取值范围是y<3；

（3）S△ABC=

=12-2-2-3

=5；

（4）∵C的坐标是(3，4)，

∴点D的坐标(3，-4)；

（5）设直线BD的解析式为y=kx+b，把（0,2），(3，-4)代入得

，

解得

，

∴y=-2x+2.