题目内容
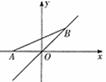
如图,点A的坐标为(-1,0),点B在直线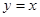 上运动,当线段AB最短时,点B的坐标为( )
上运动,当线段AB最短时,点B的坐标为( )
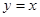 上运动,当线段AB最短时,点B的坐标为( )
上运动,当线段AB最短时,点B的坐标为( )
| A.(0,0) | B.( , , ) ) |
C.( , , ) ) | D.( , , ) ) |
B
试题分析:先过点A作AB′⊥OB,垂足为点B′,由于点B在直线y=x上运动,所以△AOB′是等腰直角三角形,由勾股定理求出OB′的长即可得出点B′的坐标.
先过点A作AB′⊥OB,垂足为点B′,由垂线段最短可知,当B′与点B重合时AB最短,

∵点B在直线y=x上运动,
∴△AOB′是等腰直角三角形,
过B′作B′C⊥x轴,垂足为C,
∴△B′CO为等腰直角三角形,
∵点A的坐标为(-1,0),
 ,
,∴B′坐标为(
 ,
, )
)故选B.
点评:解答本题的关键找到表示B′点坐标所在的等腰直角三角形.

练习册系列答案
相关题目
 与
与 分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数关系图像,假设两种灯的使用寿命都是2000h,照明效果一样.
分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数关系图像,假设两种灯的使用寿命都是2000h,照明效果一样. 
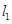 的函数关系式为
的函数关系式为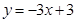 ,且
,且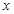 轴交于点
轴交于点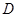 ,直线
,直线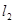 经过点
经过点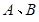 ,直线
,直线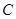 .
.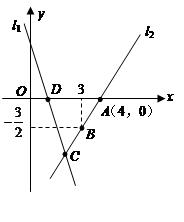
 ,梯形APCD的面积为
,梯形APCD的面积为 .
.




 的图象不经过第三象限,则
的图象不经过第三象限,则 0,
0, 0.
0.
 ,并说明理由。
,并说明理由。