题目内容
如图,直线y=kx+6与x轴、y轴分别交于点E、F,点E的坐标为,点A的坐标为(-6,0).

(1)求k的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点,在点P的运动过程中,试求出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当点P运动到什么位置时,△OPA的面积为 ,并说明理由。
,并说明理由。

(1)求k的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点,在点P的运动过程中,试求出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当点P运动到什么位置时,△OPA的面积为
 ,并说明理由。
,并说明理由。(1) ;(2)
;(2) ;(3)
;(3)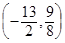
 ;(2)
;(2) ;(3)
;(3)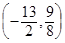
试题分析:(1)把点E(-8,0)代入
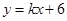 ,即可得到结果;
,即可得到结果;(2)由(1)可把y表示为含x的代数式,再根据三角形的面积公式即可面积S与x的函数关系式,根据第二象限内的直线的坐标特征即可得到自变量x的取值范围;
(3)把
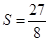 代入(2)中的函数关系式即可解出结果.
代入(2)中的函数关系式即可解出结果.(1) 把点E(-8,0)代入
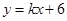 得:
得: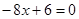 ,解得
,解得 ;
;(2) 由(1)得
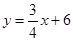 ,
,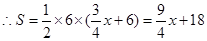
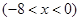 ;
;(3)当
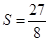 时,
时,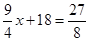 ,解得
,解得 ,
,则
 ,
,当点P运动到
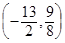 时,△OPA的面积为
时,△OPA的面积为 .
.点评:解答本题的关键是熟练掌握待定系数法求函数关系式,三角形的面积公式。

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 的图像上( )
的图像上( ) 地出发向
地出发向 地行走,同时晓阳从
地行走,同时晓阳从 分别表示小明、晓阳离A地的距离
分别表示小明、晓阳离A地的距离 (千米)与已用时间
(千米)与已用时间 (分钟)之间的关系,
(分钟)之间的关系,
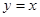 上运动,当线段AB最短时,点B的坐标为( )
上运动,当线段AB最短时,点B的坐标为( )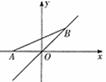
 ,
, )
) ,
, )
)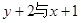 成正比例,当
成正比例,当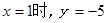
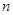 为正整数).
为正整数).