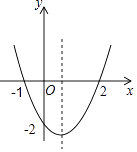ћвƒњƒЏ»Ё
°Њћвƒњ°њ»зЌЉ1£ђ‘Џ∆љ√ж÷±љ«„ш±кѕµ÷–£ђ÷±ѕя![]() ”л
”л![]() ÷бљї”Џµг
÷бљї”Џµг![]() £ђ”л
£ђ”л![]() ÷бљї”Џµг
÷бљї”Џµг![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђЈ÷±р“‘
£ђЈ÷±р“‘![]() £ђ
£ђ![]() ќ™±я„чЊЎ–ќ
ќ™±я„чЊЎ–ќ![]() £ђ÷±ѕя
£ђ÷±ѕя![]() љї
љї![]() ”Џµг
”Џµг![]() £ђљї÷±ѕя
£ђљї÷±ѕя![]() ”Џµг
”Џµг![]() £Ѓ
£Ѓ

£®1£©«у÷±ѕя![]() µƒљвќц љЉ∞
µƒљвќц љЉ∞![]() µгµƒ„ш±к£Ѓ
µгµƒ„ш±к£Ѓ
£®2£©»зЌЉ2£ђ![]() ќ™÷±ѕя
ќ™÷±ѕя![]() …ѕ“їґѓµг£ђ
…ѕ“їґѓµг£ђ![]() µг£ђ
µг£ђ![]() µгќ™÷±ѕя
µгќ™÷±ѕя![]() …ѕЅљґѓµг£®
…ѕЅљґѓµг£®![]() ‘Џ…ѕ£ђ
‘Џ…ѕ£ђ![]() ‘Џѕ¬£©£ђ¬ъ„г
‘Џѕ¬£©£ђ¬ъ„г![]() £ђµ±
£ђµ±![]() „оіу ±£ђ«у
„оіу ±£ђ«у![]() µƒ„о–°÷µ£ђ≤Ґ«у≥ціЋ ±
µƒ„о–°÷µ£ђ≤Ґ«у≥ціЋ ±![]() µгµƒ„ш±к£Ѓ
µгµƒ„ш±к£Ѓ
£®3£©»зЌЉ3£ђљЂ![]() »∆„≈µг
»∆„≈µг![]() Ћ≥ ±’л–э„™
Ћ≥ ±’л–э„™![]() £ђЉ«–э„™Їуµƒ»эљ«–ќќ™
£ђЉ«–э„™Їуµƒ»эљ«–ќќ™![]() £ђѕяґќ
£ђѕяґќ![]() Ћщ‘Џµƒ÷±ѕяљї÷±ѕя
Ћщ‘Џµƒ÷±ѕяљї÷±ѕя![]() ”Џµг
”Џµг![]() £®
£®![]() ≤ї”л
≤ї”л![]() °Ґ
°Ґ![]() ÷ЎЇѕ£©£ђљї
÷ЎЇѕ£©£ђљї![]() ÷б”Џµг
÷б”Џµг![]() £ђ‘Џ∆љ√жƒЏ «Јсіж‘Џ“їµг
£ђ‘Џ∆љ√жƒЏ «Јсіж‘Џ“їµг![]() £ђ єµ√“‘
£ђ єµ√“‘![]() Ћƒµг–ќ≥…µƒЋƒ±я–ќќ™Ѕв–ќ£ђ»фіж‘Џ£ђ«л÷±љ”–і≥ц
Ћƒµг–ќ≥…µƒЋƒ±я–ќќ™Ѕв–ќ£ђ»фіж‘Џ£ђ«л÷±љ”–і≥ц![]() µгµƒ„ш±к£ї»ф≤їіж‘Џ£ђ«лЋµ≥цјн”…£Ѓ
µгµƒ„ш±к£ї»ф≤їіж‘Џ£ђ«лЋµ≥цјн”…£Ѓ
°Њір∞Є°њ£®1£©![]() £ђH(
£ђH(![]() ,
,![]() )£ї£®2£©
)£ї£®2£©![]() £ї£®3£©іж‘Џ£ђQ(
£ї£®3£©іж‘Џ£ђQ(![]() ,
,![]() )
)
°Њљвќц°њ
£®1£©»зЌЉ1÷–£ђ„чHK°ЌOA”ЏK£Ѓ«у≥цA£ђCЅљµг„ш±к£ђјы”√іэґ®ѕµ эЈ®«у≥ц÷±ѕяACµƒљвќц љ£ђљв÷±љ«»эљ«–ќ«у≥цHK£ђKOЉіњ…«у≥цµгHµƒ„ш±к£Ѓ
£®2£©”…ћв“в|PC-PB|°№BC£ђЌ∆≥цµ±µгP‘ЏCBµƒ—”≥§ѕя…ѕ ±£ђ|PC-PB|µƒ÷µ„оіу£ђіЋ ±P°д£®3£ђ![]() £©£ђ„чP°дG°ќAC£ђ єµ√P°дG=EF=
£©£ђ„чP°дG°ќAC£ђ єµ√P°дG=EF=![]() £ђіЋ ±
£ђіЋ ±![]() £ђ„чGєЎ”Џ÷±ѕяACµƒґ‘≥∆µгM£ђЅђљ”DMљїAC”ЏE£ђGMљїAC”Џ
£ђ„чGєЎ”Џ÷±ѕяACµƒґ‘≥∆µгM£ђЅђљ”DMљїAC”ЏE£ђGMљїAC”Џ![]() £ђіЋ ±P°дF+EF+DEµƒ÷µ„о–°£Ѓ«у≥ц÷±ѕяDM£ђACµƒљвќц љ£ђєєљ®Јљ≥ћ„йЉіњ…љвЊцќ ћв£Ѓ
£ђіЋ ±P°дF+EF+DEµƒ÷µ„о–°£Ѓ«у≥ц÷±ѕяDM£ђACµƒљвќц љ£ђєєљ®Јљ≥ћ„йЉіњ…љвЊцќ ћв£Ѓ
£®3£©»зЌЉ3÷–£ђµ±NC=NM ±£ђњ…µ√Ѕв–ќMNCQ£Ѓљв÷±љ«»эљ«–ќ«у≥цON£ђ«у≥цЅв–ќµƒ±я≥§Љіњ…љвЊцќ ћв£Ѓ
£®1£©»зЌЉ1÷–£ђ„чHK°ЌOA”ЏK
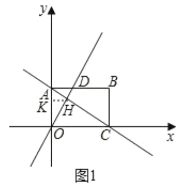
°яOA=![]() £ђOC=
£ђOC=![]() OA=3£ђ
OA=3£ђ
°аA(0£ђ![]() )£ђB(3£ђ0)£ђ
)£ђB(3£ђ0)£ђ
…и÷±ѕяACµƒљвќц љќ™y=kx+b£ђ‘т”–
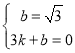
љвµ√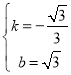
°а÷±ѕяACµƒљвќц љќ™![]()
°яtan°ѕOAC=![]()
°а°ѕOAC=![]()
°яOD°ЌAC”ЏH£ђ
°а°ѕAHO=![]()
°а°ѕAOH=![]()
°аOH=OAcos![]() =
=![]()
°яHK°ЌOA£ђ
°аHK=![]() OH=
OH=![]() £ђOK=
£ђOK=![]() HK=
HK=![]()
°аH(![]() £ђ
£ђ![]() )£Ѓ
)£Ѓ
є ір∞Єќ™£Ї![]() £ђH(
£ђH(![]() £ђ
£ђ![]() )
)
£®2£©»зЌЉ2÷–£ђ
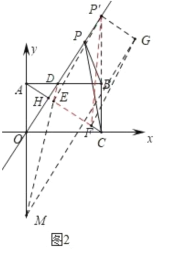
°я|PCPB|BC£ђ
°аµ±µгP‘ЏCBµƒ—”≥§ѕя…ѕ ±£ђ|PCPB|µƒ÷µ„оіу£ђіЋ ±P°д(3£ђ![]() )£ђ
)£ђ
„чP°дG°ќAC£ђ єµ√P°дG=EF=![]() £ђіЋ ±
£ђіЋ ±![]()
„чGєЎ”Џ÷±ѕяACµƒґ‘≥∆µгM£ђЅђљ”DMљїAC”ЏE£ђGMљїAC”Џ![]() £ђіЋ ±P°дF+EF+DEµƒ÷µ„о–°£Ѓ
£ђіЋ ±P°дF+EF+DEµƒ÷µ„о–°£Ѓ
°яGJ=JM£ђ…иM(m£ђn)£ђ
‘т”–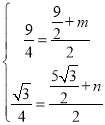
љвµ√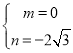
°аM(0£ђ![]() )£ђ°яD(1£ђ
)£ђ°яD(1£ђ![]() )£ђ
)£ђ
°а÷±ѕяDMµƒљвќц љќ™![]()
”…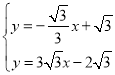
љвµ√
°а![]()
є ір∞Єќ™£Ї![]()
£®3£©»зЌЉ3÷–£ђ
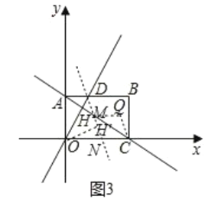
µ±NC=NM ±£ђњ…µ√Ѕв–ќMNCQ
°яNC=NM£ђ
°а°ѕNCM=°ѕNMC=![]()
°а°ѕONM=°ѕNCM+°ѕNMC=![]()
°яOH°д=OH=![]() £ђ
£ђ
°аON=OH°дcos![]() =
=![]() £ђ
£ђ
°аCN=CQ=HN=HQ=3![]() £ђ
£ђ
°аQ(![]() £ђ
£ђ![]() )
)
є ір∞Є£Їіж‘Џ£ђQ(![]() £ђ
£ђ![]() )
)

°Њћвƒњ°њљсƒк5‘¬12»’ «ќ“єъµЏ11Єц»ЂєъЈј‘÷Љх‘÷»’£ђ÷Ў«мƒ≥÷–—Іќ™∆’Љ∞Ќ∆єг»Ђ√сЈј‘÷Љх‘÷÷™ ґЇЌ±№‘÷„‘Њ»ЉЉƒ№£ђњ™’єЅЋ°∞ћбЄя‘÷Ї¶Јј÷ќƒ№Ѕ¶£ђєє÷ю…ъ√ь∞≤»ЂЈјѕя°±÷™ ґЊЇ»ьїоґѓ£Ѓ≥х“ї°Ґ≥хґюƒкЉґЄч500»Ћ£ђќ™ЅЋµч≤йЊЇ»ь«йњц£ђ—І–£љш––ЅЋ≥й—щµч≤й£ђєэ≥ћ»зѕ¬£ђ«лЄщЊЁ±нЄсїЎірќ ћв£Ѓ
’Љѓ эЊЁ£Ї
і”≥х“ї°Ґ≥хґюƒкЉґЄч≥й»°20√ыЌђ—Іµƒ≤в ‘≥…Љ®£®µ•ќї£ЇЈ÷£©£ђЉ«¬Љ»зѕ¬£Ї
≥х“ї£Ї68°Ґ79°Ґ100°Ґ98°Ґ98°Ґ86°Ґ88°Ґ99°Ґ100°Ґ93°Ґ90°Ґ100°Ґ80°Ґ76°Ґ84°Ґ98°Ґ99°Ґ86°Ґ98°Ґ90
≥хґю£Ї92°Ґ89°Ґ100°Ґ99°Ґ98°Ґ94°Ґ100°Ґ62°Ґ100°Ґ86°Ґ75°Ґ98°Ґ89°Ґ100°Ґ100°Ґ68°Ґ79°Ґ100°Ґ92°Ґ89
’ыјн эЊЁ£Ї
±н“ї
Ј÷ эґќ |
|
|
|
|
≥х“ї»Ћ э | 1 |
|
| 12 |
≥хґю»Ћ э | 2 | 2 | 4 | 12 |
Ј÷ќц эЊЁ£Ї
±нґю
÷÷ја | ∆љЊщ э | ÷–ќї э | ÷Џ э | |
≥х“ї | 90.5 | 91.5 |
| 84.75 |
≥хґю | 90.5 |
| 100 | 123.05 |
µ√≥цљб¬џ£Ї
£®1£©‘Џ±н÷–£Ї![]() _______£ђ
_______£ђ![]() _______£ђ
_______£ђ![]() _______£ђ
_______£ђ![]() _______£ї
_______£ї
£®2£©µ√Ј÷«йњцљѕќ»ґ®µƒ «___________£®ћо≥х“їїт≥хґю£©£ї
£®3£©єјЉ∆Є√–£≥х“ї°Ґ≥хґюƒкЉґ—І…ъ±Њіќ≤в ‘≥…Љ®÷–њ…“‘µ√¬ъЈ÷µƒ»Ћ эє≤”–ґа…ў»Ћ£њ