题目内容
【题目】如图，有一长方形纸片ABCD，AB=10，AD=6，将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F，求△CEF的面积．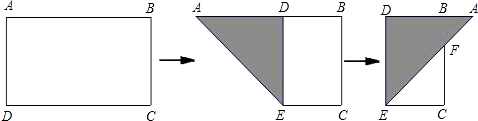 
【答案】解：如下图所示：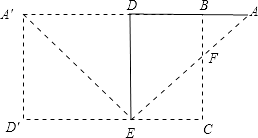 
由对称的性质可知：A′D′=A′D=AD=6，BD=10﹣6=4，
∴AB=6﹣4=2．
易证Rt△ADE∽Rt△ABF，
∴ 
∴BF= 
= 
=2
∴S△CEF= 
ABBF= ×2×2=2，
即：△CEF的面积为2．
【解析】由翻折变换（轴对称）的性质可知：AD=6，BD=10﹣6=4，AB=6﹣4=2，再证明Rt△ADE∽Rt△ABF，从而得出BF的长，由此可计算出△CEF的面积．
【考点精析】掌握翻折变换（折叠问题）是解答本题的根本，需要知道折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
练习册系列答案
智慧小复习系列答案
相关题目
【题目】团体购买公园门票票价如下：
购票人数（人） | 1～50 | 51～100 | 100以上 |
每人门票（元） | 13 | 11 | 9 |
今有甲、乙两个旅行团，已知甲团人数少于50人，乙团人数不超过100人．若分别购票，两团共计应付门票费1392元，若合在一起作为一个团体购票，总计应付门票费1080元．
（1）请你判断乙团的人数是否也少于50人；
（2）求甲、乙两旅行团各有多少人？