题目内容
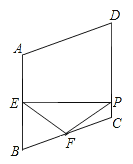
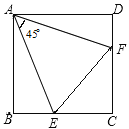
【题目】如图,在正方形ABCD中,点E在BC上,点F在CD上,连接AE、AF、EF,∠EAF=45°,BE=3,CF=4,则正方形的边长为__________.
【答案】6
【解析】
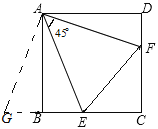
延长CB至点G,使BG=DF,并连接AG,证明△ABG≌△ADF,△AEG≌△AEF,设正方形边长为x,在Rt△CEF中应用勾股定理进行求解.
如图,延长CB至点G,使BG=DF,并连接AG,
在△ABG和△ADF中, ,
,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠GAB=∠DAF,
∵∠EAF=45°,
∴∠BAE+∠DAF=∠BAE+∠GAB=∠GAE=45°,
∴∠EAF=∠GAE,
在△AEG和△AEF中,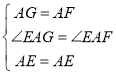 ,
,
∴△AEG≌△AEF(SAS),
∴GE=EF,
设正方形边长为x,则BG=DF=x-4,GE=EF=x-1,CE=x-3,
在Rt△CEF中,![]() ,
,
解得,![]() ,
,
∴正方形的边长为6,
故答案为:6.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目