题目内容
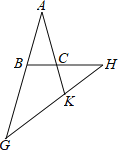
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,BD平分∠ABC,交AC于点D,AF⊥BD,垂足为点E,交BC于点F.求证:AD=CF.

【答案】见解析
【解析】
作辅助线,证明∠BAG=∠C=45°,再利用同角的余角相等得∠ABG=∠CAF,证明△ABG≌△CAF(ASA),得到AG=CF,最后证明△GAE≌△DAE(ASA),等量代换即可解题.
证明:过点A作∠BAC的平分线AG,交BD于点G,

∵AB=AC,
∴∠ABC=∠C.
∵∠BAC=90°,
∴∠ABC=∠C=45°.
∵AG平分∠BAC,
∴∠BAG=∠CAG=![]() ∠ABC=45°,
∠ABC=45°,
∴∠BAG=∠C.
∵AE⊥BD,
∴∠ABG+∠BAE=90°.
∵∠CAF+∠BAE=90°,
∴∠ABG=∠CAF.
在△ABG和△CAF中, ,
,
∴△ABG≌△CAF(ASA),
∴AG=CF.

∵BD平分∠ABC,
∴∠ABG=∠CAF,
∴∠CAF=22.5°.
∵∠CAG=45°,
∴∠GAE=∠CAG-∠CAF=45-22.5°=22.5°,
∴∠GAE=∠CAF.
∵AE⊥BD,
∴∠AEG=∠AED=90°.
在△GAE和△DAE中, ,
,
∴△GAE≌△DAE(ASA),
∴AG=AD.
∵AG=CF,
∴AD=CF.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
【题目】海洋馆的门票价格规定如表:
购票人数(人) | 150人 | 51100人 | 100人以上 |
门票单价(元/人) | 60 | 55 | 50 |
某校七年级一、二两班共102人去游公园,其中一班人数较多,经计算,如果两班都以班为单位分别购买与实际人数相同的票,则一共应付5850元。
请根据以上信息解答下列问题:
①两班各有多少学生?
②如果两班作为一个团体购票,可以节省多少钱?