Question

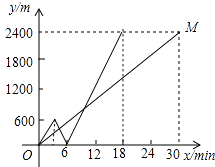
【题目】如图①，C地位于A，B两地之间，甲步行直接从C地前往B地，乙骑自行车由C地先回A地，再从A地前往B地（在A地停留时间忽略不计）．已知两人同时出发且速度不变，乙的速度是甲的2.5倍，设出发xmin后甲、乙两人离C地的距离分别为y1m，y2m，图②中线段OM表示y1与x的函数图象．

（1）甲的速度为m/min，乙的速度为m/min；
（2）在图②中画出y2与x的函数图象；
（3）求甲乙两人相遇的时间；
（4）在上述过程中，甲乙两人相距的最远距离为m．

Answer 1

【答案】
（1）80；200
（2）解：600÷200=3（min），

600×2÷200=6（min）．

2400÷200+6=18（min）．

∴y2与x的函数图象过点（0，0）、（3，600）、（6，0）、（18，2400）．

画出图形如图所示．

（3）解：设甲乙两人相遇的时间为xmin，

依题意得：80x=200（x﹣6），

解得：x=10．

答：甲乙两人相遇的时间为10min

（4）960
【解析】解：（1）甲的速度为：2400÷30=80（m/min）；
乙的速度为：80×2.5=200（m/min）．
所以答案是：80；200．（4）∵乙的速度＞甲的速度，
∴当x=3时，乙达到A地，此时甲乙两人间距可能最远，
3×（80+200）=840（m）；
当x=18时，甲乙两人间距为：
2400﹣80×18=960（m）．
∵960＞840，
∴甲乙两人相距的最远距离为960m．
所以答案是：960．