题目内容
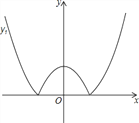
【题目】如图1,Rt△ABC中,∠ACB=Rt∠,AC=8,BC=6,点D为AB的中点,动点P从点A出发,沿AC方向以每秒1个单位的速度向终点C运动,同时动点Q从点C出发,以每秒2个单位的速度先沿CB方向运动到点B,再沿BA方向向终点A运动,以DP,DQ为邻边构造PEQD,设点P运动的时间为t秒.
(1)当t=2时,求PD的长;
(2)如图2,当点Q运动至点B时,连结DE,求证:DE∥AP.
(3)如图3,连结CD.
①当点E恰好落在△ACD的边上时,求所有满足要求的t值;
②记运动过程中PEQD的面积为S,PEQD与△ACD的重叠部分面积为S1,当![]() <
<![]() 时,请直接写出t的取值范围是 ______ .
时,请直接写出t的取值范围是 ______ .
【答案】(1)![]() (2)证明见解析(3)①分三种情况讨论:满足要求的t的值为
(2)证明见解析(3)①分三种情况讨论:满足要求的t的值为![]() 或
或![]() 或
或![]() .②当
.②当![]() <
<![]() 时, t的取值范围是
时, t的取值范围是![]() <t<
<t<![]() .
.
【解析】(1)如图1中,作DF⊥CA于F,
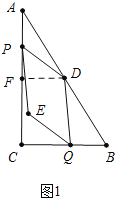
当t=2时,AP=2,DF=ADsinA=5×![]() =3,
=3,
∵AF=ADcosA=5×![]() =4,
=4,
∴PF=4-2=2,
∴PD=![]() =
=![]() =
=![]() .
.
(2)如图2中,
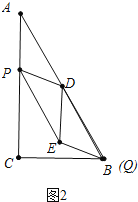
在平行四边形PEQD中,
∵PE∥DQ,
∴PE∥AD,
∵AD=DQ.PE=DQ,
∴PE=AD,
∴四边形APED是平行四边形,
∴DE∥AP.
(3)①分三种情况讨论:
Ⅰ.当点E在CA上时,
DQ⊥CB(如图3所示),
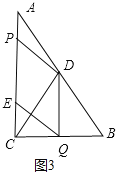
∵∠ACB=Rt∠,CD是中线,∴CD=BD,∴CQ=![]() CB=3即:t=
CB=3即:t=![]()
Ⅱ.当点E在CD上,且点Q在CB上时 (如图4所示),
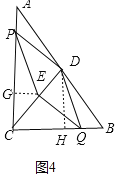
过点E作EG⊥CA于点G,过点D作DH⊥CB于点H,
易证Rt△PGE≌Rt△PHQ,∴PG=DH=4,
∴CG=4-t,GE=HQ=CQ-CH=2t-3,
∵CD=AD,∴∠DCA=∠DAC
∴在Rt△CEG中,tan∠ECG=![]() =
=![]() =
=![]() ,∴t=
,∴t=![]()
Ⅲ.当点E在CD上,且点Q在AB上时(如图5所示),过点E作EF⊥CA于点F,
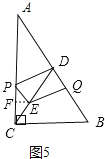
∵CD=AD,∴∠CAD=∠ACD.
∵PE∥AD,∴∠CPE=∠CAD=∠ACD,∴PE=CE,
∴PF=![]() PC=
PC=![]() ,PE=DQ=11-2t,
,PE=DQ=11-2t,
∴在Rt△PEF中,cos∠EPF=![]() =
=![]() =
=![]()
∴t=![]()
综上所述,满足要求的t的值为![]() 或
或![]() 或
或![]() .
.
②如图6中,PE交CD于E′,作E′G′⊥AC于G′,EG⊥AC于G.
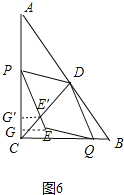
当△PDE′的面积等于平行四边形PEDQD的面积的![]() 时,PE′:EE′=2:1,
时,PE′:EE′=2:1,
由(Ⅱ)可知CG=4-t,GE=2t-3,
∴PG=8-t-(4-t)=4,
∵E′G′∥EG,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴PG′=![]() ,E′G′=
,E′G′=![]() (2t-3),CG′=8-t-
(2t-3),CG′=8-t-![]() =
=![]() -t,
-t,
∵tan∠ECG=![]() =
=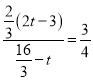 ,
,
解得t=![]() .
.
如图7中,当点Q在AB上时,PE交CD于E′,作E′G′⊥AC于G′.
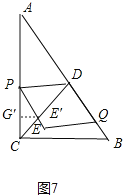
∵△PDE′的面积等于平行四边形PEDQD的面积的![]() ,
,
∴PE′:EE′=2:1,
由Ⅲ可知,PG′=![]() PC=4-
PC=4-![]() t,PE′=
t,PE′=![]() DQ=
DQ=![]() (11-2t),
(11-2t),
∵cos∠E′PG′=![]() =
=![]() ,
,
∴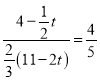 ,
,
解得t=![]() ,
,
综上所述,当![]() <
<![]() 时,请直接写出t的取值范围是
时,请直接写出t的取值范围是![]() <t<
<t<![]() .
.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案