题目内容
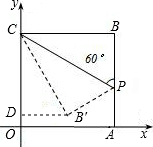
如图，在平面直角坐标系中,四边形OABC是正方形，点A的坐标是(4，0)，点P为边AB上一点，∠CPB=
，沿CP折叠正方形折叠后，点B落在平面内
处,则的坐标为（ ）
，沿CP折叠正方形折叠后，点B落在平面内处,则的坐标为（ ）A． | B． | C． | D． |
C
过点B′作B′D⊥OC ∵∠CPB=60°，CB′=OC=OA=4∴∠B′CD=30°，B′D=2
根据勾股定理得DC=2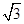
∴OD=4-2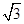，即B′点的坐标为（2，4-2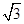）故选C．
根据勾股定理得DC=2
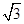∴OD=4-2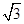，即B′点的坐标为（2，4-2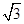）故选C．
练习册系列答案
相关题目
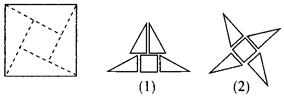
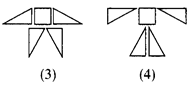
EAF绕着四边形ABCD的顶点A顺时针旋转，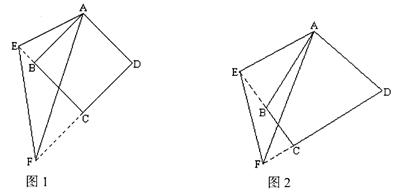
时，EF与DF、BE之间有怎样的数量关系？（只需直接写出结论）
CEF的周长（直接写出结果即可）。
