��Ŀ����
����Ŀ����ͼ![]() ����ƽ��ֱ������ϵ
����ƽ��ֱ������ϵ![]() �У�һ�κ���
�У�һ�κ���![]() ��ͼ����
��ͼ����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ������Ϊ
������Ϊ![]() ������
������![]() ��
��
��![]() ����֤��
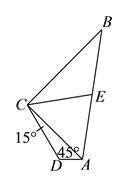
����֤��![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��![]() ����
����![]() ���߶�
���߶�![]() ���ӳ����ϣ�����
���ӳ����ϣ�����![]() ����
����![]() �Ĵ�ֱƽ���ߣ�����Ϊ��
�Ĵ�ֱƽ���ߣ�����Ϊ��![]() ������
������![]() �ύ�ڵ�
�ύ�ڵ�![]() ���ֱ�����
���ֱ�����![]() ��
��![]() ��
��
����ͼ![]() ����
����![]() ��ֱ��д��
��ֱ��д��![]() �Ķ�����
�Ķ�����
������![]() ���߶�
���߶�![]() ���ӳ������˶���
���ӳ������˶���![]() ���
���![]() ���غϣ���
���غϣ���![]() �Ķ����Ƿ�仯�����仯����˵�����ɣ������䣬���
�Ķ����Ƿ�仯�����仯����˵�����ɣ������䣬���![]() �Ķ�����
�Ķ�����
��![]() ���ڣ�
���ڣ�![]() ���������£�����
���������£�����![]() �ӵ�
�ӵ�![]() ������
������![]() ���ӳ����������˶����ٶ�Ϊÿ��
���ӳ����������˶����ٶ�Ϊÿ��![]() ����λ���ȣ�
����λ���ȣ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() �����Ϊ
�����Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() ��
��![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() ��ʱ����
��ʱ����![]() ����
����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
���𰸡���1������������2����120�����ڲ��䣬120������![]() ��y=
��y=![]() (t>0)��
(t>0)��
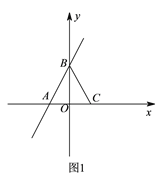
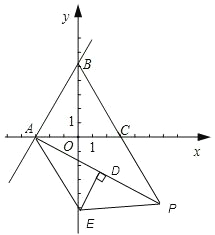
�����������������(1) �����A��B���㣬�ٸ�����������깫ʽ���AB=BC=AC�����֤��ABCΪ�ȱ������Σ�
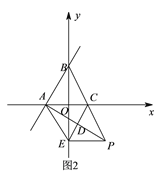
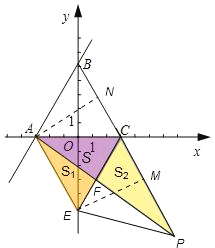
��2��������Ϊ��ABCΪ�ȱ������Σ�CP=AC��DE��AP���д��ߣ���C��D��E���㹲�ߣ���������ı���AEPC�����Σ�������⣻
������E��y���ϣ���E��AC�Ĵ�ֱƽ�����ϣ�����EA=EC���ʡ�ECA=��EAC����E��AP�Ĵ�ֱƽ�����ϣ�ͬ�������EA=EP����EC=EP=EA����ô��ECP=��EPC���ɣ�1��֪��ACP=��ECA+��ECP=120�㣬��ô��EAC����EPC�Ķ�����Ҳ��120�㣬�ɴ˿���á�AEP=360��-240��=120�㣬����AEP�Ķ������䣮
��3������S1��S2�������ֱ���������˿���S1��S2����������ֵ�������ʵ����οɵã�S1+S��ACF������S2+S��ACF������S1��S2��ֵ���ɡ�ACE�͡�ACP���������ã���E��EM��PC��M���ɣ�2��֪��ECP�ǵ��������Σ���CM=PM=![]() ����Rt��BEM�У���EBM=30�㣬BM=6+
����Rt��BEM�У���EBM=30�㣬BM=6+![]() ��ͨ����ֱ�������μ������BE�ij����Ӷ��ɵõ�OE�ij������ˣ��ɸ��������ε������ʽ��ʾ����ACE�͡�ACP��������Ӷ����S1��S2�ı���ʽ���ɴ˵ý⣮
��ͨ����ֱ�������μ������BE�ij����Ӷ��ɵõ�OE�ij������ˣ��ɸ��������ε������ʽ��ʾ����ACE�͡�ACP��������Ӷ����S1��S2�ı���ʽ���ɴ˵ý⣮
���������
��1����һ�κ���y=![]() x+3
x+3![]() ��
��
��A����3��0����B��0��3![]() ����C��3��0����
����C��3��0����
�����������빫ʽ�ɵó���AB=BC=AC=6��
���ABCΪ�ȱ������Σ�
��2���٣�����CD��������ã�C��D��E���㹲�ߣ�
��E����y���ϣ���A��C����y��Գƣ�
��E�����߶�AC�Ĵ�ֱƽ�����ϣ�
��EA=EC��
��E�����߶�AP�Ĵ�ֱƽ�����ϣ���EA=EP��
��EA=EP=EC��
���EAC=��ECA����ECP=��EPC��
�ߡ�BCA=60��������ACP=��ECA+��ECP=120�㣬
���EAC+��EPC=120��������EAC+��EPC+��ACP=240�㣬
���AEP=120�㣮
������EC��
��E����y���ϣ���A��C����y��Գƣ�
��E�����߶�AC�Ĵ�ֱƽ�����ϣ�
��EA=EC��
��E�����߶�AP�Ĵ�ֱƽ�����ϣ���EA=EP��
��EA=EP=EC��
���EAC=��ECA����ECP=��EPC��
�ߡ�BCA=60��������ACP=��ECA+��ECP=120�㣬
���EAC+��EPC=120��������EAC+��EPC+��ACP=240�㣬
�ʡ�AEP=360�㩁240��=120�㣬
���AEP�Ķ������ᷢ���仯����Ϊ120�㣮
��3����ͼ����E��EM��BP��M����A��AN��BP��N��
�ɣ�2��֪����CEP�ǵ��������Σ����У�
CM=MP=![]() CP=
CP=![]() ��
��
��BM=BC+CM=6+![]() ��
��
��Rt��BEM����MBE=30��������BE=![]() BM=
BM=![]() ��
��
��OE=BE��OB=![]() ��3
��3![]() =
=![]() +
+![]() t��
t��
��S��AEC=![]() ACOE=
ACOE=![]() ��6����
��6����![]() +
+![]() t��=3
t��=3![]() +
+![]() t��
t��
S��ACP=![]() PCAN=
PCAN=![]() ��t��3
��t��3![]() =
=![]() t��
t��
��S��AEC=S1+S��S��ACP=S+S2��
��S��AEC��S��ACP=S1+S����S2+S��=S1��S2
=3![]() +
+![]() t��
t��![]() t=3
t=3![]() ��
��![]() t��
t��
��y=3![]() ��
��![]() t��
t��
![]()

����Ŀ����֪������y=ax2+bx+c��x�ύ��A����2��0����B��4��0�����㣬����C��x��ľ���Ϊ2����������ߵĽ���ʽΪ______��
����Ŀ����һ�������ĺ�����װ��ֻ����ɫ��ͬ�ĺڡ���������40����С��������ʵ�飬�����������������Ⱥ�����������һ���������ɫ���ٰ����Żغ����У������ظ��������̣��±���ʵ���е�һ��ͳ�����ݣ�
����Ĵ���n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
��������Ĵ���m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
���������Ƶ�� | 0.63 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
��1������ƣ���ʵ�����Ϊ10000��ʱ�����������Ƶ�ʽ���ӽ��� ��������ȷ��0.1��
��2��������������һ�Σ�����������ĸ���P����������=�� ����
��3������������� ������